قانون احتمال کامل

در آمار و احتمالات قانون احتمال کامل به شرح زیر است:
که Pr ( A ∣ N ) احتمال شرطی A است در صورتی که N دانسته شده باشد.
حالت خاص قانون احتمال کامل، قانون گزینه هاست که در متغیرهای تصادفی گسسته معتبر است. این قانون می گوید اگر { Bn  : n = 1, 2, 3, . . . }حاصل از تقسیم فضای احتمال B بر n قسمت متنهای یا نامتنهای و قابل شمارش باشد، و هر 'Bn قابل شمارش باشد. آنگاه:
یا به بیان دیگر:
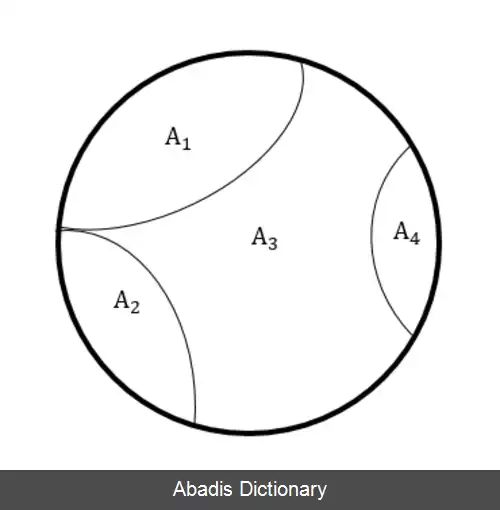
فرض کنید مجموعه U را می خواهیم به زیرمجموعه هایی A 1 , A 2 , . . . . , A n تقسیم کنیم. در اینصورت داریم:
برای افرازها و مجموعه کل یک سری قوانین وجود دارد که شامل عبارت های زیر است:
• A i ≠ ∅ , 1 ≤ i ≤ n {\displaystyle A_{i}\neq \emptyset , 1\leq i\leq n}
• A 1 ∪ A 2 ∪ . . . . ∪ A n = U {\displaystyle A_{1}\cup A_{2}\cup . . . . \cup A_{n}=U}
• A i ∩ A j = ∅ , i ≠ j , 1 ≤ i , j ≤ n {\displaystyle A_{i}\cap A_{j}=\emptyset , i\neq j, 1\leq i, j\leq n}
پیشامد رو آمدن را با F   و پیشامد پشت آمدن را با B   نشان می دهیم.
فضای نمونه برابر است با: S = { F , B }
حالا شرط های افراز می بینیم:
• F ≠ ∅ , B ≠ ∅ {\displaystyle F\neq \emptyset , B\neq \emptyset }
• F ∪ B = S {\displaystyle F\cup B=S}
• F ∩ B = ∅ {\displaystyle F\cap B=\emptyset }
قانون احتمال کل «سیده فاطمه موسوی نطنزی»
• احتمالات
• قضیه های احتمالات
• قوانین آماری
• مقاله های دارای پیوند با میان ویکی