فضای توپولوژیک ( به انگلیسی: Topological space ) مبحثی در ریاضیات است. در توپولوژی و شاخه های مربوط به آن در ریاضیات، یک فضای توپولوژیک یک مجموعه از نقاط است، همراه با مجموعه ای از همسایگی ها برای هر نقطه، که از مجموعه ای از اصول که نقاط را به همسایه ها مرتبط می کنند، پیروی می کند. تعریف فضای توپولوژیک بر نظریه مجموعه ها استوار است و عمومی ترین مفهوم برای فضاهای ریاضی است که اجازه می دهد بتوان مفاهیمی مانند پیوستگی، حد دنباله ها و فضای همبند را تعریف کرد. دیگر فضاها، خمینهها و فضاهای متریک، حالت های خاص شده ای از فضای توپولوژیک با ساختارهای اضافه تر یا محدودتر هستند. شاخه ای از ریاضیات که فضای توپولوژیک را به عنوان اصول پایه خود مورد مطالعه قرار می دهد، توپولوژی عمومی نام دارد.
سودمندی مفهوم یک توپولوژی، با این حقیقت نشان داده می شود که چندین تعریف معادل برای این ساختار وجود دارد. بنابراین هر یک از آن ها می تواند به عنوان چند اصل طبقه بندی شده برای یک کاربرد خاص یا آنچه مورد نیاز است، انتخاب شود. پراستفاده ترین و ظریف ترین این تعاریف، تعریف با استفاده از مجموعه های باز است. اما قابل درک ترین آن ها، تعریف با همسایگی هاست.
فرض کنید X یک مجموعه باشد. اعضای X معمولاً نقاط نامیده می شوند هرچند که می توانند هر شیء ریاضی دیگر باشند. همچنین X می تواند تهی باشد. فرض کنید N یک تابع باشد که هر x ( نقطه ) از X را به یک گردایه ناتهی ( N ( x از زیرمجموعه های X نسبت دهد. اعضای ( N ( x همسایه های x نامیده می شود. تابع N همسایگی نامیده می شود اگر از چهار اصل زیر پیروی کند؛ آن گاه X با N یک فضای توپولوژیک نامیده می شود. فضای توپولوژیکی که در آن نقاط همان توابع باشند، یک فضای تابعی نام دارد.
• اگر N یک همسایگی x باشد ( یعنی ( N ∈ N ( x ) ، آن گاه x ∈ N باشد. به عبارت دیگر، هر نقطه به هر یک از همسایگی های خود تعلق داشته باشد.
• اگر N زیر مجموعه ای از X و شامل همسایگی های x باشد، آن گاه N یک همسایگی x باشد. یعنی هر فرامجموعه از یک همسایگی نقطه x در X خود یک همسایگی برای x باشد.
• اشتراک هر دو همسایگی از x، خود یک همسایگی از x باشد.
• هر همسایگی N از x شامل همسایگی M از x است به طوری که N یک همسایگی برای هر نقطه از M باشد.
سه اصل ابتدایی مفهوم روشنی دارند. اصل چهارم استفاده خیلی مهمی در ساختار این تئوری دارد، که همان ارتباط بین همسایگی های مختلف یک نقطه است. مثال استاندارد برای سیستم همسایگی ها خط اعداد حقیقی است که در آن زیر مجموعه N از R یک همسایگی از عدد حقیقی x است، اگر یک بازهٔ باز وجود داشته باشد که نقطه x را شامل شود و نیز مشمول N باشد.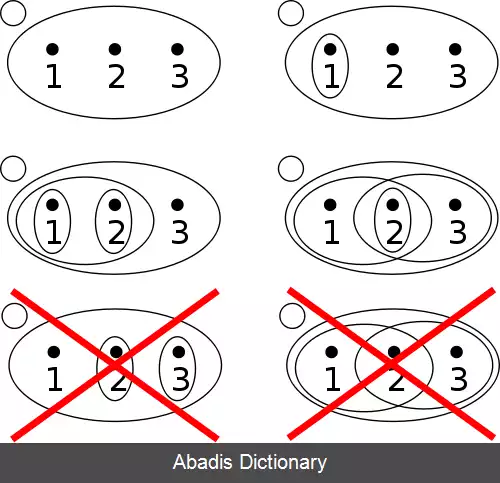
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفسودمندی مفهوم یک توپولوژی، با این حقیقت نشان داده می شود که چندین تعریف معادل برای این ساختار وجود دارد. بنابراین هر یک از آن ها می تواند به عنوان چند اصل طبقه بندی شده برای یک کاربرد خاص یا آنچه مورد نیاز است، انتخاب شود. پراستفاده ترین و ظریف ترین این تعاریف، تعریف با استفاده از مجموعه های باز است. اما قابل درک ترین آن ها، تعریف با همسایگی هاست.
فرض کنید X یک مجموعه باشد. اعضای X معمولاً نقاط نامیده می شوند هرچند که می توانند هر شیء ریاضی دیگر باشند. همچنین X می تواند تهی باشد. فرض کنید N یک تابع باشد که هر x ( نقطه ) از X را به یک گردایه ناتهی ( N ( x از زیرمجموعه های X نسبت دهد. اعضای ( N ( x همسایه های x نامیده می شود. تابع N همسایگی نامیده می شود اگر از چهار اصل زیر پیروی کند؛ آن گاه X با N یک فضای توپولوژیک نامیده می شود. فضای توپولوژیکی که در آن نقاط همان توابع باشند، یک فضای تابعی نام دارد.
• اگر N یک همسایگی x باشد ( یعنی ( N ∈ N ( x ) ، آن گاه x ∈ N باشد. به عبارت دیگر، هر نقطه به هر یک از همسایگی های خود تعلق داشته باشد.
• اگر N زیر مجموعه ای از X و شامل همسایگی های x باشد، آن گاه N یک همسایگی x باشد. یعنی هر فرامجموعه از یک همسایگی نقطه x در X خود یک همسایگی برای x باشد.
• اشتراک هر دو همسایگی از x، خود یک همسایگی از x باشد.
• هر همسایگی N از x شامل همسایگی M از x است به طوری که N یک همسایگی برای هر نقطه از M باشد.
سه اصل ابتدایی مفهوم روشنی دارند. اصل چهارم استفاده خیلی مهمی در ساختار این تئوری دارد، که همان ارتباط بین همسایگی های مختلف یک نقطه است. مثال استاندارد برای سیستم همسایگی ها خط اعداد حقیقی است که در آن زیر مجموعه N از R یک همسایگی از عدد حقیقی x است، اگر یک بازهٔ باز وجود داشته باشد که نقطه x را شامل شود و نیز مشمول N باشد.

wiki: فضای توپولوژی
