در ریاضیات، فیزیک، و مهندسی، فضای برداری ( یا فضای خطی ) ( به انگلیسی: Vector Space ) به مجموعه ای از اشیاء به نام بردار گفته می شود که روی آنها دو عمل «جمع» و «ضرب اسکالر در بردار» تعریف شده باشد. این اسکالر معمولاً عددی حقیقی است، اما در حالت کلی می توان آن را عضو هر میدانی مانند اعداد مختلط در نظر گرفت. این دو عمل باید طوری تعریف شده باشند که چند قاعده یا اصل موضوع را برآورند. برای مشخص کردن این که اسکالر ضرب نرده ای، حقیقی ست یا مختلط، از عبارت های فضای برداری حقیقی یا فضای برداری مختلط استفاده می شود. [ ۱]
مجموعهٔ بردارهای اقلیدسی نمونه ای از فضای برداری است. از بردارهای اقلیدسی در نمایش کمیت های برداری در فیزیک استفاده می شود. برای پیدا کردن نیروی خالص وارد بر یک جسم، همهٔ نیروهای وارد بر آن را جمع برداری می کنیم؛ همچنین، بردار نیرو از ضرب بردار شتاب در جرم ( یک کمیت نرده ای ) به دست می آید.
در حالت کلی، بردارهای یک فضای برداری لزوماً یک بردار اقلیدسی نیستند پس لزوماً با فلش نمایش داده نمی شوند. به عبارت دیگر، بردار یک چیز انتزاعی است و تنها گاهی می توان آنها را با پیکان ( فلش ) نمایش داد.
فضاهای برداری در ریاضیات، علم و مهندسی، گسترده استفاده می شوند. در جبر خطی، از فضای برداری در کار با دستگاه های معادلات خطی استفاده می شوند. همچنین از فضاهای برداری برای حل معادلات دیفرانسیل با مشتقات جزئی و بسط فوریه استفاده می شود.
فضای برداری، سنگ بنایی برای تعمیم به چیزهای هندسی و فیزیکی کلی تر، مانند ماتریس و تنسورها هستند.
یک فضای برداری ( V , + , ⋅ ) روی یک میدان اسکالر F ( مانند میدان اعداد حقیقی R ) یک مجموعه از بردارها V به همراه دو عمل جمع و ضرب اسکالر است.
• مجموعهٔ V ≠ ∅ {\displaystyle V\neq \varnothing } ناتهی است.
• عمل جمع + : V × V → V {\displaystyle +:V\times V\rightarrow V} یک عمل دوتایی روی دو بردار از V {\displaystyle V} است.
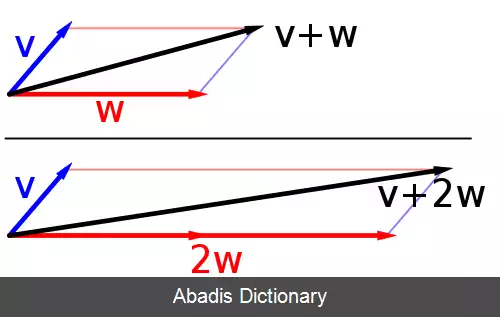
• عمل ضرب ⋅ : F × V → V {\displaystyle \cdot :F\times V\rightarrow V} یک عمل دوتایی بین یک بردار از V {\displaystyle V} و یک اسکالر از F {\displaystyle F} است. ضرب در اسکالر، نباید با ضرب داخلی اشتباه شود، در ضرب داخلی دو بردار در هم ضرب می شوند و یک اسکالر به دست می آید، درحالی که در ضرب اسکالر، یک بردار در یک اسکالر ضرب می شود و یک بردار جدید به دست می آید.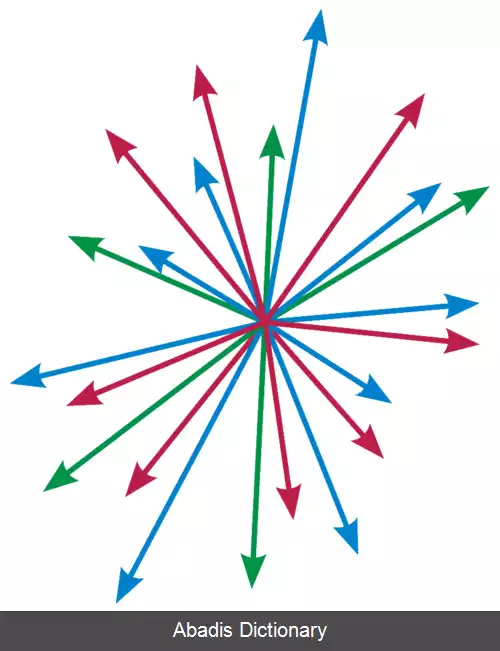
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمجموعهٔ بردارهای اقلیدسی نمونه ای از فضای برداری است. از بردارهای اقلیدسی در نمایش کمیت های برداری در فیزیک استفاده می شود. برای پیدا کردن نیروی خالص وارد بر یک جسم، همهٔ نیروهای وارد بر آن را جمع برداری می کنیم؛ همچنین، بردار نیرو از ضرب بردار شتاب در جرم ( یک کمیت نرده ای ) به دست می آید.
در حالت کلی، بردارهای یک فضای برداری لزوماً یک بردار اقلیدسی نیستند پس لزوماً با فلش نمایش داده نمی شوند. به عبارت دیگر، بردار یک چیز انتزاعی است و تنها گاهی می توان آنها را با پیکان ( فلش ) نمایش داد.
فضاهای برداری در ریاضیات، علم و مهندسی، گسترده استفاده می شوند. در جبر خطی، از فضای برداری در کار با دستگاه های معادلات خطی استفاده می شوند. همچنین از فضاهای برداری برای حل معادلات دیفرانسیل با مشتقات جزئی و بسط فوریه استفاده می شود.
فضای برداری، سنگ بنایی برای تعمیم به چیزهای هندسی و فیزیکی کلی تر، مانند ماتریس و تنسورها هستند.
یک فضای برداری ( V , + , ⋅ ) روی یک میدان اسکالر F ( مانند میدان اعداد حقیقی R ) یک مجموعه از بردارها V به همراه دو عمل جمع و ضرب اسکالر است.
• مجموعهٔ V ≠ ∅ {\displaystyle V\neq \varnothing } ناتهی است.
• عمل جمع + : V × V → V {\displaystyle +:V\times V\rightarrow V} یک عمل دوتایی روی دو بردار از V {\displaystyle V} است.
• عمل ضرب ⋅ : F × V → V {\displaystyle \cdot :F\times V\rightarrow V} یک عمل دوتایی بین یک بردار از V {\displaystyle V} و یک اسکالر از F {\displaystyle F} است. ضرب در اسکالر، نباید با ضرب داخلی اشتباه شود، در ضرب داخلی دو بردار در هم ضرب می شوند و یک اسکالر به دست می آید، درحالی که در ضرب اسکالر، یک بردار در یک اسکالر ضرب می شود و یک بردار جدید به دست می آید.


wiki: فضای برداری
