فضای برداری R k با ضرب داخلی و نرم ‖ x ‖ = ( ∑ i = 1 k x i 2 ) 1 / 2 که x = ( x 1 , x 2 , … , x k ) ∈ R k ، را فضای اقلیدسی k بعدی می نامیم.
R ، فضای اقلیدسی یک بعدی یا همان خط حقیقی است. R × R یا R 2 نیز فضای اقلیدسی دو بعدی است که به آن صفحه اقلیدسی یا دستگاه مختصات دکارتی می گوییم. با تعمیم این مفاهیم فضای اقلیدسی nبعدی یا R n و به همین ترتیب فضای اقلیدسی بینهایت بعدی، R ω تعریف می شوند.
فضاهای با بعد بالاتر در زمینه هایی مانند نسبیت، مکانیک آماری و مکانیک کوانتمی کاربرد دارند. در مکانیک کوانتمی حتی فضاهای با بعد نامتناهی نیز کاربرد دارند.
یک نقطه در فضای دو بعدی عبارت است از جفت مرتبی از عددهای حقیقی مانند ( x 1 , x 2 ) . به همین طریق یک نقطه در فضای سه بعدی، سه تایی مرتبی از عددهای حقیقی مانند ( x 1 , x 2 , x 3 ) است؛ بنابراین می توان nتایی مرتبی از عددهای حقیقی مانند ( x 1 , x 2 , … , x n ) را به عنوان نقطه ای در فضای nبعدی در نظر گرفت.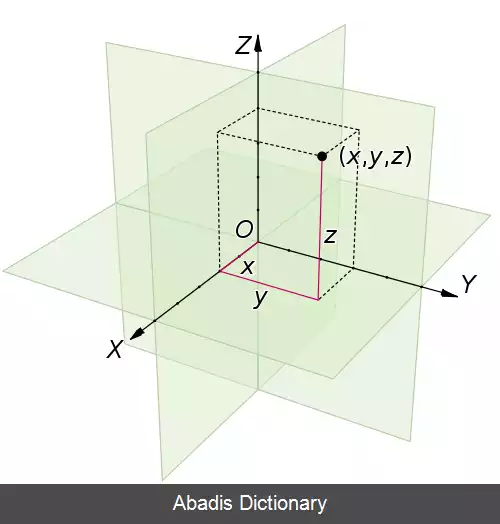
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفR ، فضای اقلیدسی یک بعدی یا همان خط حقیقی است. R × R یا R 2 نیز فضای اقلیدسی دو بعدی است که به آن صفحه اقلیدسی یا دستگاه مختصات دکارتی می گوییم. با تعمیم این مفاهیم فضای اقلیدسی nبعدی یا R n و به همین ترتیب فضای اقلیدسی بینهایت بعدی، R ω تعریف می شوند.
فضاهای با بعد بالاتر در زمینه هایی مانند نسبیت، مکانیک آماری و مکانیک کوانتمی کاربرد دارند. در مکانیک کوانتمی حتی فضاهای با بعد نامتناهی نیز کاربرد دارند.
یک نقطه در فضای دو بعدی عبارت است از جفت مرتبی از عددهای حقیقی مانند ( x 1 , x 2 ) . به همین طریق یک نقطه در فضای سه بعدی، سه تایی مرتبی از عددهای حقیقی مانند ( x 1 , x 2 , x 3 ) است؛ بنابراین می توان nتایی مرتبی از عددهای حقیقی مانند ( x 1 , x 2 , … , x n ) را به عنوان نقطه ای در فضای nبعدی در نظر گرفت.

wiki: فضای اقلیدسی
