فرایندهای تصمیم گیری مارکوف ( به انگلیسی: Markov decision process ) ( به اختصار: MDPs ) یک چارچوب ریاضی است برای مدل سازی تصمیم گیری در شرایطی که نتایج تا حدودی تصادفی و تا حدودی تحت کنترل یک تصمیم گیر است. MDPs برای مطالعه طیف گسترده ای از مسائل بهینه سازی که از طریق برنامه نویسی پویا و تقویت یادگیری حل می شوند مفید است. حداقل از اوایل ۱۹۵۰ میلادی MDPs شناخته شده است ( cf. ( Bellman 1957 ) ) . هسته اصلی پژوهش در فرایندهای تصمیم گیری مارکوف حاصل کتاب رونالد هوارد است که در سال ۱۹۶۰ تحت عنوان «برنامه نویسی پویا و فرایندهای مارکف» منتشر شد. [ ۱] فرایندهای تصمیم گیری مارکوف در طیف گسترده ای از رشته ها از جمله رباتیک، اقتصاد و تولید استفاده می شود.
به طور دقیق تر، فرایندهای تصمیم گیری مارکوف، فرایندهای کنترل تصادفی زمان گسسته است. در هر گام، فرایند در حالت s است و تصمیم گیر اقدام ( عمل ) a را انتخاب می کند. پاسخ فرایند، رفتن به حالت جدید s ( در گام بعدی ) به طور تصادفی و همچنین دادن پاداش R_a ( s, s' ) به تصمیم گیر است R a ( s , s ′ ) .
فرایندهای تصمیم گیری مارکوف شامل پنج عنصر ( S , A , P ⋅ ( ⋅ , ⋅ ) , R ⋅ ( ⋅ , ⋅ ) , γ ) است که در ادامه شرح داده می شود
• S {\displaystyle S} مجموعه متناهی ( شمارش پذیر ) حالت ها است.
• A {\displaystyle A} مجموعه متناهی عمل ها است. به طور جایگزین A s {\displaystyle A_{s}} مجموعه متناهی از عمل ها است که حالت s {\displaystyle s}
• P a ( s , s ′ ) = Pr ( s t + 1 = s ′ ∣ s t = s , a t = a ) {\displaystyle P_{a} ( s, s' ) =\Pr ( s_{t+1}=s'\mid s_{t}=s, a_{t}=a ) } احتمال این که اقدام a {\displaystyle a} در حالت s {\displaystyle s} و در زمان t {\displaystyle t} منجر به حالت s ′ {\displaystyle s'} در زمان t + 1 {\displaystyle t+1}
• R a ( s , s ′ ) {\displaystyle R_{a} ( s, s' ) } پاداش فوری ( یا انتظار پاداش فوری ) است که به علت رفتن از حالت s ′ {\displaystyle s'} به حالت s {\displaystyle s}
• γ ∈ {\displaystyle \gamma \in } ضریب کاهش است که نشان دهنده تفاوت ارزش پاداش آتی با پاداش فعلی است.
مسئله اصلی در MDPs پیدا کردن یک «سیاست» برای تصمیم گیر است. یافتن یک تابع مشخص عمل π که تصمیم گیر در هنگامی که در حالت s است انتخاب کند s . توجه داشته باشید که که افزودن یک سیاست ثابت به فرایندهای تصمیم گیری مارکوف منجر به یک زنجیره مارکوف می شود.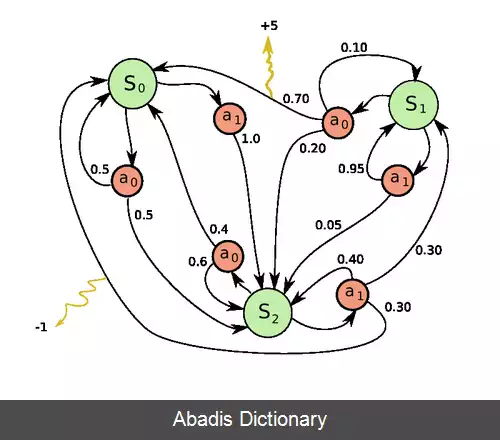
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور دقیق تر، فرایندهای تصمیم گیری مارکوف، فرایندهای کنترل تصادفی زمان گسسته است. در هر گام، فرایند در حالت s است و تصمیم گیر اقدام ( عمل ) a را انتخاب می کند. پاسخ فرایند، رفتن به حالت جدید s ( در گام بعدی ) به طور تصادفی و همچنین دادن پاداش R_a ( s, s' ) به تصمیم گیر است R a ( s , s ′ ) .
فرایندهای تصمیم گیری مارکوف شامل پنج عنصر ( S , A , P ⋅ ( ⋅ , ⋅ ) , R ⋅ ( ⋅ , ⋅ ) , γ ) است که در ادامه شرح داده می شود
• S {\displaystyle S} مجموعه متناهی ( شمارش پذیر ) حالت ها است.
• A {\displaystyle A} مجموعه متناهی عمل ها است. به طور جایگزین A s {\displaystyle A_{s}} مجموعه متناهی از عمل ها است که حالت s {\displaystyle s}
• P a ( s , s ′ ) = Pr ( s t + 1 = s ′ ∣ s t = s , a t = a ) {\displaystyle P_{a} ( s, s' ) =\Pr ( s_{t+1}=s'\mid s_{t}=s, a_{t}=a ) } احتمال این که اقدام a {\displaystyle a} در حالت s {\displaystyle s} و در زمان t {\displaystyle t} منجر به حالت s ′ {\displaystyle s'} در زمان t + 1 {\displaystyle t+1}
• R a ( s , s ′ ) {\displaystyle R_{a} ( s, s' ) } پاداش فوری ( یا انتظار پاداش فوری ) است که به علت رفتن از حالت s ′ {\displaystyle s'} به حالت s {\displaystyle s}
• γ ∈ {\displaystyle \gamma \in } ضریب کاهش است که نشان دهنده تفاوت ارزش پاداش آتی با پاداش فعلی است.
مسئله اصلی در MDPs پیدا کردن یک «سیاست» برای تصمیم گیر است. یافتن یک تابع مشخص عمل π که تصمیم گیر در هنگامی که در حالت s است انتخاب کند s . توجه داشته باشید که که افزودن یک سیاست ثابت به فرایندهای تصمیم گیری مارکوف منجر به یک زنجیره مارکوف می شود.

