فرایند پواسون ( به انگلیسی: Poisson process ) یک فرایند نقطه ای شمارشگر است که پیرامون وقوع رخدادهای تصادفی بر روی یک طول زمانی، یا یک فاصلهٔ مکانی تعریف می شود. در بررسی این فرایند زمان بین دو پیشامد متوالی را یک توزیع نمایی مشخص می کند و بازه های زمانی مجزا مستقل از هم در نظر گرفته می شوند. از این فرایند برای مدل سازی واپاشی رادیواکتیو، تماس های تلفنی و انتقال داده از سایتهای اینترنتی استفاده می شود. فرایند پواسون فرایند پیوسته در زمان است. همان طور که فرایند برنولی را گسسته در زمان نامید.
تعریف رسمی آن فرایند نقطه ای پواسون ( به انگلیسی:Poisson Point Process ( PPP ) ) است؛ اما معمولاً کلمه نقطه ای ادا نمی شود؛ در حالی که ممکن است یک بعدی نباشد، باید کلمه نقطه ای با صفحه ای یا فضایی جایگزین و ادا شود.
به علاوه؛ چون فرایند معمولاً اشاره به نوعی تکامل است، کلمه حوزه بجای فرایند بکار می رود.
چون پیشامدهای تصادفی مورد این مبحث هستند، آن را تحلیل تصادفی نیز نامیده اند.
به فرایند شمارشگر { N ( t ) ; t ⩾ 0 } فرایند پواسون با نرخ λ > 0 , گفته می شود اگر که داشته باشیم:
• N ( 0 ) = 0 {\displaystyle N ( 0 ) =0}
• فرایند افزایشی مستقل باشد.
• تعداد رویدادهای اتفاق افتاده در بازهٔ زمانی به طول τ {\displaystyle \tau } به صورت پواسون توزیع شده است و میانگین λ τ {\displaystyle \lambda \tau } دارد. در واقع برای تمام t {\displaystyle t} ها، به ازای τ ⩾ 0 {\displaystyle \tau \geqslant 0}
P r { N ( t + τ ) − N ( t ) = k } = e − λ τ ( λ τ ) k k ! k = 0 , 1 , … ,
از مورد سوم داریم : E = λ τ که در واقع توضیح می دهد که چرا نرخ فرایند است.
فرایند همگن پواسون با پارامتر λ مشخص می شود که به نوعی شدت را نشان می دهد. تعداد پیشامدها در یک بازه زمانی ( t, t + τ] از توزیع پواسون با پارامتر λτ پیروی می کند.
که N در این رابطه N ( t + τ ) - N ( t ) = k تعداد پیشامدها را در بازه زمانی نشان می دهد ( t, t + τ].
همان طور که یک متغیر تصادفی با توزیع پواسون را با پارامتر λ مشخص می شود، فرایند پواسون همگن نیز با پارامتر λ مشخص می شود که امید ریاضی تعداد پیشامدها را در واحد زمان نشان می دهد.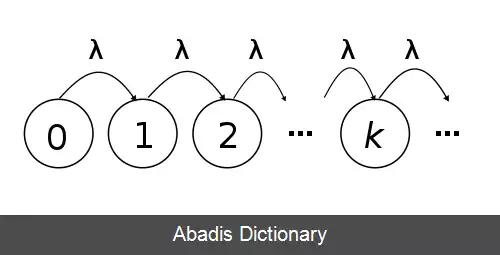
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتعریف رسمی آن فرایند نقطه ای پواسون ( به انگلیسی:Poisson Point Process ( PPP ) ) است؛ اما معمولاً کلمه نقطه ای ادا نمی شود؛ در حالی که ممکن است یک بعدی نباشد، باید کلمه نقطه ای با صفحه ای یا فضایی جایگزین و ادا شود.
به علاوه؛ چون فرایند معمولاً اشاره به نوعی تکامل است، کلمه حوزه بجای فرایند بکار می رود.
چون پیشامدهای تصادفی مورد این مبحث هستند، آن را تحلیل تصادفی نیز نامیده اند.
به فرایند شمارشگر { N ( t ) ; t ⩾ 0 } فرایند پواسون با نرخ λ > 0 , گفته می شود اگر که داشته باشیم:
• N ( 0 ) = 0 {\displaystyle N ( 0 ) =0}
• فرایند افزایشی مستقل باشد.
• تعداد رویدادهای اتفاق افتاده در بازهٔ زمانی به طول τ {\displaystyle \tau } به صورت پواسون توزیع شده است و میانگین λ τ {\displaystyle \lambda \tau } دارد. در واقع برای تمام t {\displaystyle t} ها، به ازای τ ⩾ 0 {\displaystyle \tau \geqslant 0}
P r { N ( t + τ ) − N ( t ) = k } = e − λ τ ( λ τ ) k k ! k = 0 , 1 , … ,
از مورد سوم داریم : E = λ τ که در واقع توضیح می دهد که چرا نرخ فرایند است.
فرایند همگن پواسون با پارامتر λ مشخص می شود که به نوعی شدت را نشان می دهد. تعداد پیشامدها در یک بازه زمانی ( t, t + τ] از توزیع پواسون با پارامتر λτ پیروی می کند.
که N در این رابطه N ( t + τ ) - N ( t ) = k تعداد پیشامدها را در بازه زمانی نشان می دهد ( t, t + τ].
همان طور که یک متغیر تصادفی با توزیع پواسون را با پارامتر λ مشخص می شود، فرایند پواسون همگن نیز با پارامتر λ مشخص می شود که امید ریاضی تعداد پیشامدها را در واحد زمان نشان می دهد.

wiki: فرایند پواسون
