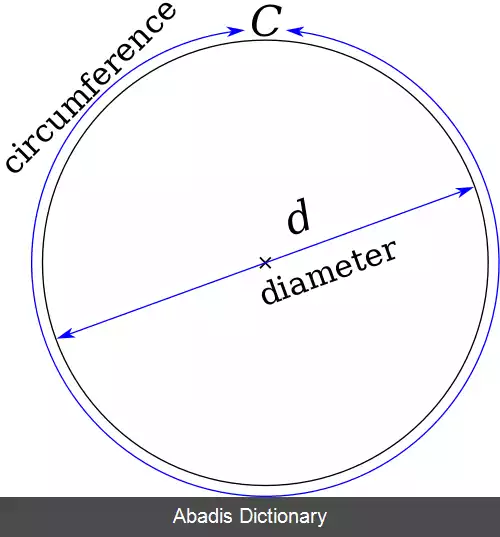
عدد پی ( π ) ، یک ثابت ریاضیاتی است. این ثابت به صورت نسبت محیط دایره به قطرش تعریف شده و تعاریف معادل مختلفی نیز دارد. این عدد در بسیاری از فرمول های ریاضیاتی، در تمام زمینه های ریاضیات و فیزیک ظاهر می شود. قدیمی ترین استفاده از حرف یونانی π جهت نمایش نسبت محیط دایره به قطرش، توسط ریاضیدان ویلزی به نام ویلیام جونز در ۱۷۰۶ میلادی بر می گردد. [ ۱] این ثابت تقریباً برابر با ۳٫۱۴۱۵۹ بوده و برخی مواقع به آن ثابت ارشمیدس هم گفته می شود. [ ۲] [ ۳] [ ۴]
از آنجا که π یک عدد گنگ است، نمی توان آن را به صورت کسر متعارفی بیان کرد، گرچه که کسرهایی چون 22 7 را اغلب جهت تخمین آن به کار می برند. گنگ بودن آن را می توان به طور معادل اینگونه بیان کرد: نمایش مبنای ده ( دسیمال ) آن پایان ناپذیر بوده و هیچگاه الگوی تا ابد تکرار شونده ای نخواهد داشت. ارقام مبنای ده ( و مبناهای دیگر ) آن ظاهراً تصادفی بوده و حدس زده می شود که در نوع خاصی از تصادفی بودن آماری صدق می کند.
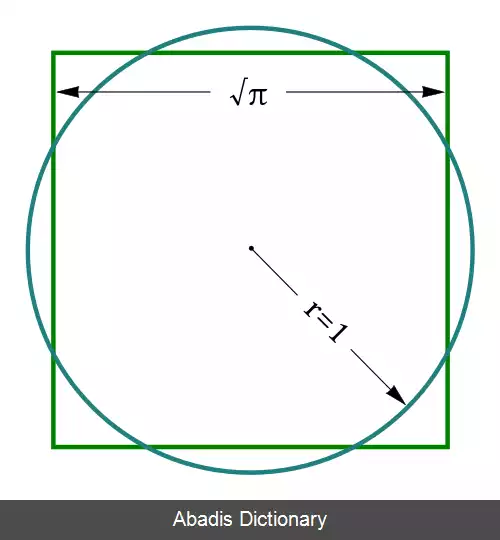
مشخص شده که π یک عدد متعالی است:[ ۳] یعنی ریشه هیچ چندجمله ای با ضرایب گویا نیست. متعالی بودن π ایجاب می کند که حل چالش باستانی تربیع دایره با خط کش و پرگار غیرممکن باشد. این عدد در محیط و مساحت دایره و در سطح و حجم استوانه، کره، مخروط استفاده می گردد.
تمدن های باستانی شامل مصریان و بابلیان، نیاز به تخمین های نسبتاً دقیقی از π برای محاسبات عملی داشتند. حدود ۲۵۰ قبل از میلاد بود که ریاضیدان یونانی به نام ارشمیدس، الگوریتمی را جهت تخمین π با دقت دلخواه ایجاد کرد. در قرن پنجم بعد از میلاد، ریاضیدانان چینی عدد π را تا هفت رقم اعشار تخمین زدند، در حالی که ریاضیدانان هندی به تخمین پنج رقمی دست یافته و هردو نیز از فنون هندسی در این تخمین ها بهره جستند. اولین فرمول دقیق برای π ، بر اساس سری های نامتناهی بود که هزار سال بعد کشف شد. این کشف در ریاضیات هند و طی کشف سری ماداوا - لایبنیتس ( Madhava - Leibniz ) حاصل شد. [ ۵] [ ۶] ( عدد پی برابر با ۳. ۱۴ است ) به زودی، ابداع حسابان منجر به محاسبه صدها رقم از π شد که جهت استفاده در تمامی انواع محاسبات علمی کفایت می کرد. با این حال، در قرن ۲۰م و ۲۱م میلادی، ریاضیدانان و دانشمندان کامپیوتری به دنبال رهیافت های تازه ای رفته اند که در ترکیب با افزایش قدرت محاسباتی، نمایش ارقام π را به چندین تریلیون رقم توسعه داده اند. [ ۷] [ ۸] در حقیقت انگیزه اولیه و اصلی محاسبات جهت یافتن ارقام عدد π ، تبدیل این فرایند به نمونه آزمایشی جهت توسعه الگوریتم های کارا برای محاسبه سری های عددی، و همچنین عطش شکستن رکوردهاست. [ ۹] [ ۱۰] چنین محاسبات گسترده ای که در این فرایند به کار می رود، جهت آزمودن سوپرکامپیوترها و الگوریتم های ضرب با دقت بالا نیز به کار رفته اند.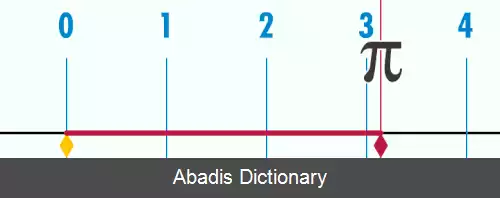

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز آنجا که π یک عدد گنگ است، نمی توان آن را به صورت کسر متعارفی بیان کرد، گرچه که کسرهایی چون 22 7 را اغلب جهت تخمین آن به کار می برند. گنگ بودن آن را می توان به طور معادل اینگونه بیان کرد: نمایش مبنای ده ( دسیمال ) آن پایان ناپذیر بوده و هیچگاه الگوی تا ابد تکرار شونده ای نخواهد داشت. ارقام مبنای ده ( و مبناهای دیگر ) آن ظاهراً تصادفی بوده و حدس زده می شود که در نوع خاصی از تصادفی بودن آماری صدق می کند.
مشخص شده که π یک عدد متعالی است:[ ۳] یعنی ریشه هیچ چندجمله ای با ضرایب گویا نیست. متعالی بودن π ایجاب می کند که حل چالش باستانی تربیع دایره با خط کش و پرگار غیرممکن باشد. این عدد در محیط و مساحت دایره و در سطح و حجم استوانه، کره، مخروط استفاده می گردد.
تمدن های باستانی شامل مصریان و بابلیان، نیاز به تخمین های نسبتاً دقیقی از π برای محاسبات عملی داشتند. حدود ۲۵۰ قبل از میلاد بود که ریاضیدان یونانی به نام ارشمیدس، الگوریتمی را جهت تخمین π با دقت دلخواه ایجاد کرد. در قرن پنجم بعد از میلاد، ریاضیدانان چینی عدد π را تا هفت رقم اعشار تخمین زدند، در حالی که ریاضیدانان هندی به تخمین پنج رقمی دست یافته و هردو نیز از فنون هندسی در این تخمین ها بهره جستند. اولین فرمول دقیق برای π ، بر اساس سری های نامتناهی بود که هزار سال بعد کشف شد. این کشف در ریاضیات هند و طی کشف سری ماداوا - لایبنیتس ( Madhava - Leibniz ) حاصل شد. [ ۵] [ ۶] ( عدد پی برابر با ۳. ۱۴ است ) به زودی، ابداع حسابان منجر به محاسبه صدها رقم از π شد که جهت استفاده در تمامی انواع محاسبات علمی کفایت می کرد. با این حال، در قرن ۲۰م و ۲۱م میلادی، ریاضیدانان و دانشمندان کامپیوتری به دنبال رهیافت های تازه ای رفته اند که در ترکیب با افزایش قدرت محاسباتی، نمایش ارقام π را به چندین تریلیون رقم توسعه داده اند. [ ۷] [ ۸] در حقیقت انگیزه اولیه و اصلی محاسبات جهت یافتن ارقام عدد π ، تبدیل این فرایند به نمونه آزمایشی جهت توسعه الگوریتم های کارا برای محاسبه سری های عددی، و همچنین عطش شکستن رکوردهاست. [ ۹] [ ۱۰] چنین محاسبات گسترده ای که در این فرایند به کار می رود، جهت آزمودن سوپرکامپیوترها و الگوریتم های ضرب با دقت بالا نیز به کار رفته اند.






wiki: عدد پی
