در نظریه اعداد، عدد مودب ( به انگلیسی: Polite Number ) یا عدد پلکانی ( به انگلیسی: Staircase Number ) عدد صحیح مثبتی است که حاصل جمع دو یا چند عدد صحیح مثبت متوالی است. اعداد مودب را از آن رو پلکانی می گویند که بازنمود بصری بسط مودبانهٔ یک عدد مودب همانند یک پلکان است.
۳ = ۱ + ۲
۵ = ۲ + ۳
۶ = ۱ + ۲ + ۳
۷ = ۳ + ۴
۹ = ۴ + ۵ = ۲ + ۳ + ۴
۱۰ = ۱ + ۲ + ۳ + ۴
۱۱ = ۵ + ۶
۱۲ = ۳ + ۴ + ۵
۱۳ = ۶ + ۷
۱۴ = ۲ + ۳ + ۴ + ۵
۱۵ = ۷ + ۸ = ۴ + ۵ + ۶ = ۱ + ۲ + ۳ + ۴ + ۵
۱۷ = ۸ + ۹
۱۸ = ۵ + ۶ + ۷ = ۳ + ۴ + ۵ + ۶
۱۹ = ۹ + ۱۰
۲۰ = ۲ + ۳ + ۴ + ۵ + ۶
دنبالهٔ اعداد مودب دنباله ای است نامتناهی از اعداد صحیح که در آن توان های عدد ۲ جایی ندارد:
۳، ۵، ۶، ۷، ۹، ۱۰، ۱۱، ۱۲، ۱۳، ۱۴، ۱۵، ۱۷، ۱۸، ۱۹، ۲۰، ۲۱، ۲۲، ۲۳، ۲۴، ۲۵، ۲۶، ۲۷، ۲۸، ۲۹، ۳۰، ۳۱، ۳۳، ۳۴، ۳۵، ۳۶، ۳۷، ۳۸، ۳۹، ۴۰، ۴۱، ۴۲، ۴۳، ۴۴، ۴۵، ۴۶، ۴۷، ۴۸، ۴۹، ۵۰، . . . [ ۱]
n اُمین عدد مودب برابر است با f ( n + 1 ) آنجا که f ( n ) = n + ⌊ log 2 ( n + log 2 n ) ⌋
به تعداد دفعاتی که می توان یک عدد صحیح مثبت را به صورت حاصل جمع دو یا چند عدد صحیح مثبت متوالی نشان داد ادب آن عدد می گویند. برای مثال ادب عدد ۷ برابر با یک و عدد ۱۵ برابر با ۳ است. مفهوم ادب اعداد صحیح خود تشکیل دنباله ای نامتناهی می دهد که به شکل زیر است:
۰، ۰، ۱، ۰، ۱، ۱، ۱، ۰، ۲، ۱، ۱، ۱، ۱، ۱، ۳، ۰، ۱، ۲، ۱، ۱، ۳، ۱، ۱، ۱، ۲، ۱، ۳، ۱، ۱، ۳، ۱، ۰، ۳، ۱، ۳، ۲، ۱، ۱، ۳، ۱، ۱، ۳، ۱، ۱، ۵، ۱، ۱، ۱، ۲، . . . [ ۲]
برای هر عدد صحیح و مثبت x، ادب x برابر است با تعداد مقسوم علیههای فرد بزرگتر از یک آن عدد[ ۳] .
به هر عدد صحیح و مثبت که توانی از عدد 2 است یک عدد نامودب گفته می شود زیرا نمی توان این اعداد را به صورت حاصل جمع چند عدد صحیح مثبت متوالی بسط داد. اعداد نامودب نیز دنباله ای نامتناهی تشکیل می دهند.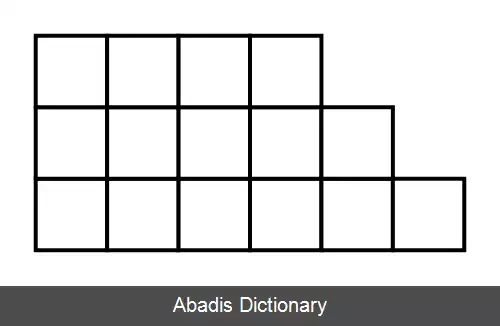
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف۳ = ۱ + ۲
۵ = ۲ + ۳
۶ = ۱ + ۲ + ۳
۷ = ۳ + ۴
۹ = ۴ + ۵ = ۲ + ۳ + ۴
۱۰ = ۱ + ۲ + ۳ + ۴
۱۱ = ۵ + ۶
۱۲ = ۳ + ۴ + ۵
۱۳ = ۶ + ۷
۱۴ = ۲ + ۳ + ۴ + ۵
۱۵ = ۷ + ۸ = ۴ + ۵ + ۶ = ۱ + ۲ + ۳ + ۴ + ۵
۱۷ = ۸ + ۹
۱۸ = ۵ + ۶ + ۷ = ۳ + ۴ + ۵ + ۶
۱۹ = ۹ + ۱۰
۲۰ = ۲ + ۳ + ۴ + ۵ + ۶
دنبالهٔ اعداد مودب دنباله ای است نامتناهی از اعداد صحیح که در آن توان های عدد ۲ جایی ندارد:
۳، ۵، ۶، ۷، ۹، ۱۰، ۱۱، ۱۲، ۱۳، ۱۴، ۱۵، ۱۷، ۱۸، ۱۹، ۲۰، ۲۱، ۲۲، ۲۳، ۲۴، ۲۵، ۲۶، ۲۷، ۲۸، ۲۹، ۳۰، ۳۱، ۳۳، ۳۴، ۳۵، ۳۶، ۳۷، ۳۸، ۳۹، ۴۰، ۴۱، ۴۲، ۴۳، ۴۴، ۴۵، ۴۶، ۴۷، ۴۸، ۴۹، ۵۰، . . . [ ۱]
n اُمین عدد مودب برابر است با f ( n + 1 ) آنجا که f ( n ) = n + ⌊ log 2 ( n + log 2 n ) ⌋
به تعداد دفعاتی که می توان یک عدد صحیح مثبت را به صورت حاصل جمع دو یا چند عدد صحیح مثبت متوالی نشان داد ادب آن عدد می گویند. برای مثال ادب عدد ۷ برابر با یک و عدد ۱۵ برابر با ۳ است. مفهوم ادب اعداد صحیح خود تشکیل دنباله ای نامتناهی می دهد که به شکل زیر است:
۰، ۰، ۱، ۰، ۱، ۱، ۱، ۰، ۲، ۱، ۱، ۱، ۱، ۱، ۳، ۰، ۱، ۲، ۱، ۱، ۳، ۱، ۱، ۱، ۲، ۱، ۳، ۱، ۱، ۳، ۱، ۰، ۳، ۱، ۳، ۲، ۱، ۱، ۳، ۱، ۱، ۳، ۱، ۱، ۵، ۱، ۱، ۱، ۲، . . . [ ۲]
برای هر عدد صحیح و مثبت x، ادب x برابر است با تعداد مقسوم علیههای فرد بزرگتر از یک آن عدد[ ۳] .
به هر عدد صحیح و مثبت که توانی از عدد 2 است یک عدد نامودب گفته می شود زیرا نمی توان این اعداد را به صورت حاصل جمع چند عدد صحیح مثبت متوالی بسط داد. اعداد نامودب نیز دنباله ای نامتناهی تشکیل می دهند.

wiki: عدد مؤدب
