فرهنگستان زبان و ادب
دانشنامه عمومی
در نظریۀ اعداد، عدد تام ( به انگلیسی: Perfect Number ) ، عدد صحیح مثبتی است که برابر با مجموع مقسوم علیه های سرهٔ مثبت خود باشد. همچنین به طور هم ارز، عدد تام، عددی است که نصف مجموع همهٔ مقسوم علیه های مثبت خود باشد. [ ۱] عدد تام.
نخستین عدد تام ۶ است؛ زیرا ۱+۲+۳=۶ یا به طور هم ارز، ۶=۲/ ( ۱+۲+۳+۶ ) . بعد از آن ۲۸ و بعد از آن به ترتیب ۴۹۶ و ۸۱۲۸ قرار دارند.
این چهار عددِ یاد شده، تنها اعداد شناخته شده در ریاضیات یونانی بودند. نیکوماخوس عدد تام ۸۱۲۸ را در حدود سال ۱۰۰ پس از میلاد شناسایی کرده بود. [ ۲] در دست نوشته ای مربوط به سال های بین ۱۴۵۶ و ۱۴۶۱ یک ریاضی دان گمنام اولین بار به درستی از پنجمین عدد تام، ۳۳٬۵۵۰٬۳۳۶ یاد کرده است. در سال ۱۵۸۸، پیترو کاتالدی ریاضی دان ایتالیایی، ششمین و هفتمین اعداد تام را که به ترتیب برابر با ۸٬۵۸۹٬۸۶۹٬۰۵۶ و ۱۳۷٬۴۳۸٬۶۹۱٬۳۲۸ هستند، شناسایی کرد. [ ۳]
اقلیدس ثابت کرده است که عدد ( ۲p−1 ( ۲p−۱ یک عدد زوج تام است اگر ۲p−۱ یک عدد اول باشد. برای نمونه، چهار عدد اول یاد شده را می توان با این رابطه و با قرار دادن چهار عدد اول به برای p به دست آورد:
برای این که عدد ( ۲p−1 ( ۲p−۱ اول باشد، باید p خود یک عدد اول باشد. اعداد اول به این شکل را اعداد مرسن می نامند. مارین مرسن یک راهب فرانسوی قرن هفدهم بود که اعداد اول و اعداد تام را بررسی کرد. البته همه اعداد به شکل ( ۲p−1 ( ۲p−۱ و با p اول، اول نیستند. در واقع اعداد مرسن بسیار کمیاب هستند، از میان ۱٬۶۲۲٬۴۴۱ عدد اولی که تا ۲۵٬۹۶۴٬۹۵۱ وجود دارند، تنها ۴۲ تای آن ها را اعداد مرسن تشکیل می دهند.
بیش از هزار سال بعد از اقلیدس، حدود هزار پس از میلاد ابن هیثم بیان کرد که هر عدد تام زوج به شکل ( ۲p−1 ( ۲p−۱ است. این نتیجه تا قرن هجدهم ثابت نشده باقی ماند و در نهایت لئونارد اویلر توانست نشان دهد که همهٔ عددهای تام زوج توسط رابطهٔ ( ۲p−1 ( ۲p−۱ به ازای اعداد اول مرسن قابل تولید هستند. این نتیجه به معنای وجود یک تناظر یک به یک بین اعداد تام زوج و اعداد اول مرسن است. این قضیه به نام قضیهٔ اقلیدس - اویلر شناخته شده است. تا نوامبر ۲۰۱۲ تعداد اعداد مرسن و در نتیجه اعداد تام شناخته شده ۴۹ تاست. [ ۴] بزرگترین آن ها۲۷۴۲۰۷۲۸۱ با ۴۴٬۶۷۷٬۲۳۵ رقم است.
۴۲ عدد تام نخست را با رابطهٔ ( ۲p−1 ( ۲p−۱ به ازای ۴۲ عدد اول p تولید می شوند: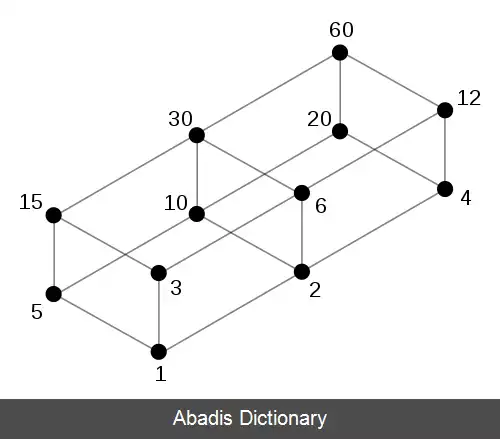
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنخستین عدد تام ۶ است؛ زیرا ۱+۲+۳=۶ یا به طور هم ارز، ۶=۲/ ( ۱+۲+۳+۶ ) . بعد از آن ۲۸ و بعد از آن به ترتیب ۴۹۶ و ۸۱۲۸ قرار دارند.
این چهار عددِ یاد شده، تنها اعداد شناخته شده در ریاضیات یونانی بودند. نیکوماخوس عدد تام ۸۱۲۸ را در حدود سال ۱۰۰ پس از میلاد شناسایی کرده بود. [ ۲] در دست نوشته ای مربوط به سال های بین ۱۴۵۶ و ۱۴۶۱ یک ریاضی دان گمنام اولین بار به درستی از پنجمین عدد تام، ۳۳٬۵۵۰٬۳۳۶ یاد کرده است. در سال ۱۵۸۸، پیترو کاتالدی ریاضی دان ایتالیایی، ششمین و هفتمین اعداد تام را که به ترتیب برابر با ۸٬۵۸۹٬۸۶۹٬۰۵۶ و ۱۳۷٬۴۳۸٬۶۹۱٬۳۲۸ هستند، شناسایی کرد. [ ۳]
اقلیدس ثابت کرده است که عدد ( ۲p−1 ( ۲p−۱ یک عدد زوج تام است اگر ۲p−۱ یک عدد اول باشد. برای نمونه، چهار عدد اول یاد شده را می توان با این رابطه و با قرار دادن چهار عدد اول به برای p به دست آورد:
برای این که عدد ( ۲p−1 ( ۲p−۱ اول باشد، باید p خود یک عدد اول باشد. اعداد اول به این شکل را اعداد مرسن می نامند. مارین مرسن یک راهب فرانسوی قرن هفدهم بود که اعداد اول و اعداد تام را بررسی کرد. البته همه اعداد به شکل ( ۲p−1 ( ۲p−۱ و با p اول، اول نیستند. در واقع اعداد مرسن بسیار کمیاب هستند، از میان ۱٬۶۲۲٬۴۴۱ عدد اولی که تا ۲۵٬۹۶۴٬۹۵۱ وجود دارند، تنها ۴۲ تای آن ها را اعداد مرسن تشکیل می دهند.
بیش از هزار سال بعد از اقلیدس، حدود هزار پس از میلاد ابن هیثم بیان کرد که هر عدد تام زوج به شکل ( ۲p−1 ( ۲p−۱ است. این نتیجه تا قرن هجدهم ثابت نشده باقی ماند و در نهایت لئونارد اویلر توانست نشان دهد که همهٔ عددهای تام زوج توسط رابطهٔ ( ۲p−1 ( ۲p−۱ به ازای اعداد اول مرسن قابل تولید هستند. این نتیجه به معنای وجود یک تناظر یک به یک بین اعداد تام زوج و اعداد اول مرسن است. این قضیه به نام قضیهٔ اقلیدس - اویلر شناخته شده است. تا نوامبر ۲۰۱۲ تعداد اعداد مرسن و در نتیجه اعداد تام شناخته شده ۴۹ تاست. [ ۴] بزرگترین آن ها۲۷۴۲۰۷۲۸۱ با ۴۴٬۶۷۷٬۲۳۵ رقم است.
۴۲ عدد تام نخست را با رابطهٔ ( ۲p−1 ( ۲p−۱ به ازای ۴۲ عدد اول p تولید می شوند:

wiki: عدد تام
دانشنامه آزاد فارسی
عدد تام (perfect number)
عدد صحیح مثبتی که برابر با مجموع مقسومٌ علیه های خود، جز خودش، باشد. به عبارت دیگر، مجموع همۀ مقسوم علیه های آن، دو برابر خودش باشد. مثلاً، ۲۸ عددی تام است، زیرا برابر است با ۱۴+۷+۴+۲+۱. اگر مجموع مقسوم علیه های یک عدد صحیح مثبت، جز خودش، کوچک تر از آن عدد باشد، عدد را ناقص می نامند و اگر بزرگ تر از آن عدد باشد، عدد را زائد می گویند. مثلاً ۸ ناقص و ۱۲ زائد است.
عدد صحیح مثبتی که برابر با مجموع مقسومٌ علیه های خود، جز خودش، باشد. به عبارت دیگر، مجموع همۀ مقسوم علیه های آن، دو برابر خودش باشد. مثلاً، ۲۸ عددی تام است، زیرا برابر است با ۱۴+۷+۴+۲+۱. اگر مجموع مقسوم علیه های یک عدد صحیح مثبت، جز خودش، کوچک تر از آن عدد باشد، عدد را ناقص می نامند و اگر بزرگ تر از آن عدد باشد، عدد را زائد می گویند. مثلاً ۸ ناقص و ۱۲ زائد است.
wikijoo: عدد_تام
مترادف ها
چیز درست، عدد صحیح، عدد درست، عدد تام
چیز درست، عدد صحیح، عدد درست، عدد تام
عدد صحیح، عدد تام
پیشنهاد کاربران
شماره رسا
