در هندسهٔ تحلیلی، ضرب داخلی ( به انگلیسی: Inner Product ) یا ضرب اسکالر ( به انگلیسی: scalar product ) یک عمل دوتایی بین دو بردار اقلیدسی است که نتیجهٔ آن یک عدد حقیقی است. به عبارتی دیگر، نتیجهٔ ضرب داخلیِ دو کمیت برداری، یک کمیت اسکالر است.
ضرب داخلی با نماد نقطه در وسط «·» نمایش داده می شود که با نقطه «. » تفاوت دارد، ازاین رو در انگلیسی به آن ضرب نقطه ای ( به انگلیسی: dot product ) هم گفته می شود. [ ۱]
ضرب داخلی دو بردار a → = ( a 1 , a 2 , … , a n ) و b → = ( b 1 , b 2 , … , b n ) در فضای R n به صورت زیر تعریف می شود:[ ۲]
a → ⋅ b → = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n
( 1 , 3 , − 5 ) ⋅ ( 4 , − 2 , − 1 ) = 1 × 4 + 3 × − 2 + − 5 × − 1 = 4 − 6 + 5 = 3
اگر بردارها را ماتریس سطری فرض کنیم ضرب داخلی را می توان از رابطهٔ زیر نیز محاسبه کرد ( b T یعنی ماتریس ترانهادهٔ b ) :
a → ⋅ b → = a b T
= 3
اگر θ زاویهٔ بین دو بردار باشد:[ ۳]
a → ⋅ b → = | a → | | b → | cos θ
در نتیجه:[ ۳]
• اگر a → {\displaystyle {\vec {a}}} و b → {\displaystyle {\vec {b}}} بر هم عمود باشند، نتیجهٔ ضرب صفر خواهد شد و برعکس: θ = 90 ∘ ⇒ cos θ = 0 ⟺ a → ⋅ b → = 0 {\displaystyle \theta =90^{\circ }\Rightarrow \cos \theta =0\Longleftrightarrow {\vec {a}}\cdot {\vec {b}}=0}
• اگر a → {\displaystyle {\vec {a}}} و b → {\displaystyle {\vec {b}}} با هم موازی باشند، نتیجهٔ ضرب برابر ضرب طول بردارها خواهد شد و برعکس: θ = 0 ⇒ cos θ = 1 ⟺ a → ⋅ b → = | a → | | b → | {\displaystyle \theta =0\Rightarrow \cos \theta =1\Longleftrightarrow {\vec {a}}\cdot {\vec {b}}=\left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert }
• ضرب داخلی یک بردار در خودش برابر مقدار طول آن به توان ۲ است: a → ⋅ a → = | a → | 2 {\displaystyle {\vec {a}}\cdot {\vec {a}}=\left\vert {\vec {a}}\right\vert ^{2}}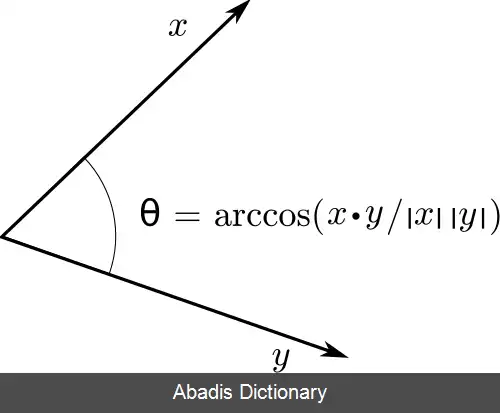
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفضرب داخلی با نماد نقطه در وسط «·» نمایش داده می شود که با نقطه «. » تفاوت دارد، ازاین رو در انگلیسی به آن ضرب نقطه ای ( به انگلیسی: dot product ) هم گفته می شود. [ ۱]
ضرب داخلی دو بردار a → = ( a 1 , a 2 , … , a n ) و b → = ( b 1 , b 2 , … , b n ) در فضای R n به صورت زیر تعریف می شود:[ ۲]
a → ⋅ b → = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n
( 1 , 3 , − 5 ) ⋅ ( 4 , − 2 , − 1 ) = 1 × 4 + 3 × − 2 + − 5 × − 1 = 4 − 6 + 5 = 3
اگر بردارها را ماتریس سطری فرض کنیم ضرب داخلی را می توان از رابطهٔ زیر نیز محاسبه کرد ( b T یعنی ماتریس ترانهادهٔ b ) :
a → ⋅ b → = a b T
= 3
اگر θ زاویهٔ بین دو بردار باشد:[ ۳]
a → ⋅ b → = | a → | | b → | cos θ
در نتیجه:[ ۳]
• اگر a → {\displaystyle {\vec {a}}} و b → {\displaystyle {\vec {b}}} بر هم عمود باشند، نتیجهٔ ضرب صفر خواهد شد و برعکس: θ = 90 ∘ ⇒ cos θ = 0 ⟺ a → ⋅ b → = 0 {\displaystyle \theta =90^{\circ }\Rightarrow \cos \theta =0\Longleftrightarrow {\vec {a}}\cdot {\vec {b}}=0}
• اگر a → {\displaystyle {\vec {a}}} و b → {\displaystyle {\vec {b}}} با هم موازی باشند، نتیجهٔ ضرب برابر ضرب طول بردارها خواهد شد و برعکس: θ = 0 ⇒ cos θ = 1 ⟺ a → ⋅ b → = | a → | | b → | {\displaystyle \theta =0\Rightarrow \cos \theta =1\Longleftrightarrow {\vec {a}}\cdot {\vec {b}}=\left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert }
• ضرب داخلی یک بردار در خودش برابر مقدار طول آن به توان ۲ است: a → ⋅ a → = | a → | 2 {\displaystyle {\vec {a}}\cdot {\vec {a}}=\left\vert {\vec {a}}\right\vert ^{2}}

wiki: ضرب داخلی
