در ریاضیات، ضرب خارجی ( به انگلیسی: Cross Product ) ، یا ضرب برداری ( به انگلیسی: Vector Product ) ، یک عمل دوتایی ( با نماد ×[ ۱] ) بین دو بردار اقلیدسی در فضای سه بعدی است که نتیجهٔ آن برداری است که بر هر دو بردار اولیه عمود است.
برای بردار های یکّهٔ پایه تساوی های زیر برقرار اند[ ۲] [ ۳] :
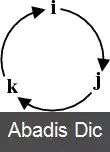
i ^ × j ^ = − j ^ × i ^ = k ^
j ^ × k ^ = − k ^ × j ^ = i ^
k ^ × i ^ = − i ^ × k ^ = j ^
i ^ × i ^ = 0 → j ^ × j ^ = 0 → k ^ × k ^ = 0 →
از تساوی های فوق می توان فرمول ضرب خارجی را نتیجه گرفت[ ۲] :
اگر a → = ( a x , a y , a z ) و b → = ( b x , b y , b z ) :
a → × b → = ( a y b z − a z b y , a z b x − a x b z , a x b y − a y b x )
برای حفظ کردن راحت تر ضرب خارجی می توان از تساوی زیر کمک گرفت[ ۲] [ ۳] :
a → × b → = | i ^ j ^ k ^ a x a y a z b x b y b z |
این دترمینان را می توان با روش ساروس محاسبه کرد که در نهایت به فرمول بیان ریاضی می رسد.
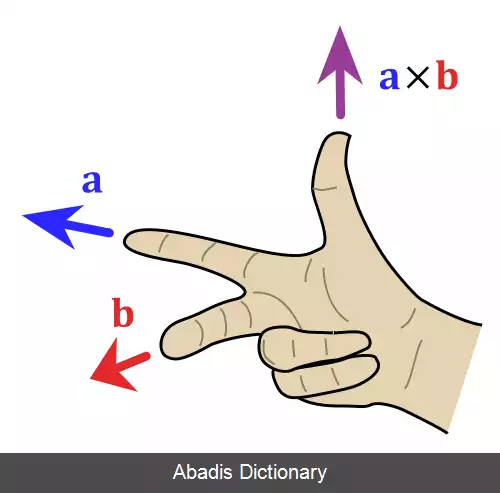
جهت بردارِ حاصل از ضرب خارجی، عمود بر هر دو بردار a → و b → است و به کمک قانون دست راست قابل تشخیص است و طول آن برابر مساحت متوازی الاضلاعی با اضلاع بردار های اوّلیّه است[ ۴] ؛ پس اگر θ زاویهٔ بین دو بردار باشد[ ۲] :
| a → × b → | = | a → | | b → | sin θ
اگر بردار ها هم راستا باشند یا یکی از بردار ها صفر باشد، حاصل ضرب خارجی صفر خواهد شد.
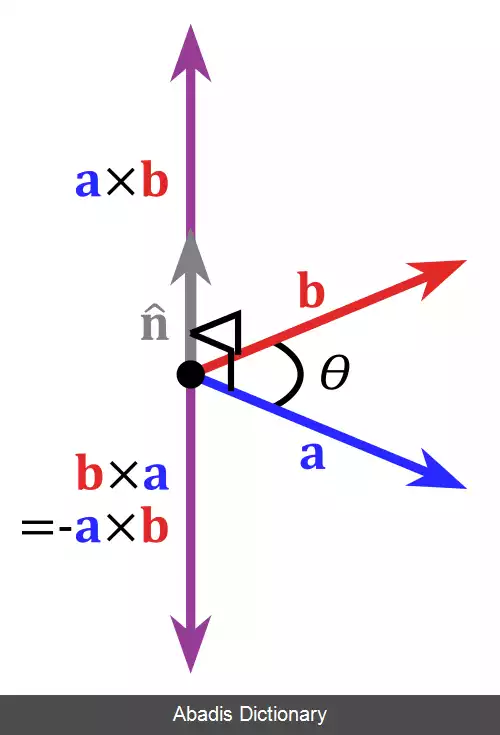
• جابه جایی ندارد ولی[ ۲] : a → × b → = − b → × a → {\displaystyle {\vec {a}}\times {\vec {b}}= - {\vec {b}}\times {\vec {a}}}
• پخش پذیری[ ۲] : a → × ( b → + c → ) = a → × b → + a → × c → {\displaystyle {\vec {a}}\times ( {\vec {b}}+{\vec {c}} ) ={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}}
• شرکت پذیری ندارد ولی از تساوی جاکوبی پیروی می کند: a → × ( b → × c → ) + b → × ( c → × a → ) + c → × ( a → × b → ) = 0 → {\displaystyle {\vec {a}}\times ( {\vec {b}}\times {\vec {c}} ) +{\vec {b}}\times ( {\vec {c}}\times {\vec {a}} ) +{\vec {c}}\times ( {\vec {a}}\times {\vec {b}} ) ={\vec {0}}}
• ضرب در عدد[ ۲] : ( r a → ) × b → = a → × ( r b → ) = r ( a → × b → ) {\displaystyle ( r{\vec {a}} ) \times {\vec {b}}={\vec {a}}\times ( r{\vec {b}} ) =r ( {\vec {a}}\times {\vec {b}} ) }
• a → × a → = 0 → {\displaystyle {\vec {a}}\times {\vec {a}}={\vec {0}}}
• a → × b → = 0 → ⟺ a → ∥ b → {\displaystyle {\vec {a}}\times {\vec {b}}={\vec {0}}\Longleftrightarrow {\vec {a}}\parallel {\vec {b}}} [ ۲]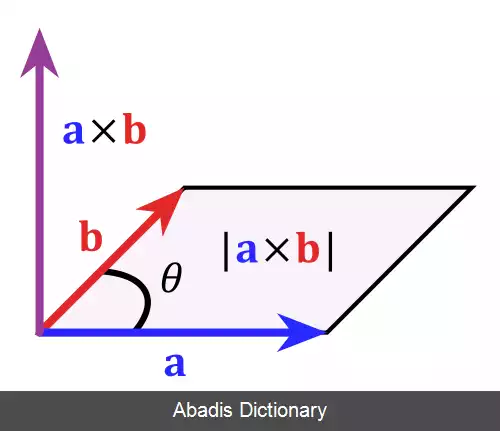
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای بردار های یکّهٔ پایه تساوی های زیر برقرار اند[ ۲] [ ۳] :
i ^ × j ^ = − j ^ × i ^ = k ^
j ^ × k ^ = − k ^ × j ^ = i ^
k ^ × i ^ = − i ^ × k ^ = j ^
i ^ × i ^ = 0 → j ^ × j ^ = 0 → k ^ × k ^ = 0 →
از تساوی های فوق می توان فرمول ضرب خارجی را نتیجه گرفت[ ۲] :
اگر a → = ( a x , a y , a z ) و b → = ( b x , b y , b z ) :
a → × b → = ( a y b z − a z b y , a z b x − a x b z , a x b y − a y b x )
برای حفظ کردن راحت تر ضرب خارجی می توان از تساوی زیر کمک گرفت[ ۲] [ ۳] :
a → × b → = | i ^ j ^ k ^ a x a y a z b x b y b z |
این دترمینان را می توان با روش ساروس محاسبه کرد که در نهایت به فرمول بیان ریاضی می رسد.
جهت بردارِ حاصل از ضرب خارجی، عمود بر هر دو بردار a → و b → است و به کمک قانون دست راست قابل تشخیص است و طول آن برابر مساحت متوازی الاضلاعی با اضلاع بردار های اوّلیّه است[ ۴] ؛ پس اگر θ زاویهٔ بین دو بردار باشد[ ۲] :
| a → × b → | = | a → | | b → | sin θ
اگر بردار ها هم راستا باشند یا یکی از بردار ها صفر باشد، حاصل ضرب خارجی صفر خواهد شد.
• جابه جایی ندارد ولی[ ۲] : a → × b → = − b → × a → {\displaystyle {\vec {a}}\times {\vec {b}}= - {\vec {b}}\times {\vec {a}}}
• پخش پذیری[ ۲] : a → × ( b → + c → ) = a → × b → + a → × c → {\displaystyle {\vec {a}}\times ( {\vec {b}}+{\vec {c}} ) ={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}}
• شرکت پذیری ندارد ولی از تساوی جاکوبی پیروی می کند: a → × ( b → × c → ) + b → × ( c → × a → ) + c → × ( a → × b → ) = 0 → {\displaystyle {\vec {a}}\times ( {\vec {b}}\times {\vec {c}} ) +{\vec {b}}\times ( {\vec {c}}\times {\vec {a}} ) +{\vec {c}}\times ( {\vec {a}}\times {\vec {b}} ) ={\vec {0}}}
• ضرب در عدد[ ۲] : ( r a → ) × b → = a → × ( r b → ) = r ( a → × b → ) {\displaystyle ( r{\vec {a}} ) \times {\vec {b}}={\vec {a}}\times ( r{\vec {b}} ) =r ( {\vec {a}}\times {\vec {b}} ) }
• a → × a → = 0 → {\displaystyle {\vec {a}}\times {\vec {a}}={\vec {0}}}
• a → × b → = 0 → ⟺ a → ∥ b → {\displaystyle {\vec {a}}\times {\vec {b}}={\vec {0}}\Longleftrightarrow {\vec {a}}\parallel {\vec {b}}} [ ۲]




wiki: ضرب خارجی
