شبکه ی ارجاعات یا استنادات برای مدل کردن ارجاع دادن توسط یک مقاله، به مقالات دیگر گفته می شود. این شبکه را می توان به صورت یک گراف جهت دار نشان داد که در این گراف، راس های آن مقالات نوشته شده و یال های این گراف نیز دادن ارجاع به مقاله ای دیگر است. جهت این یال نیز از مقاله ی نوشته شده به سمت مقاله ای که به آن ارجاع داده است، می باشد.
شبکه های ارجاعات برای درک تأثیر مقالات و کارهای علمی در طول زمان بسیار مهم هستند. این شبکه ها، به محققان کمک می کنند مقالات کلیدی را در هر رشته و حوزه شناسایی کنند، توسعه ایده ها را ردیابی کنند و تأثیر تحقیقات را در درون و بین رشته ها اندازه گیری کنند.
اگر گراف ارجاعات را برای مقالات یک حوزه ی علمی رسم کنیم، با نگاه کردن به این شبکه و همچنین دیدن میزان یال هایی که به هر راس این گراف متصل هستند، می توان میزان اهمیت یک مقاله در آن حوزه را متوجه شد. میزان راس های ورودی با اهمیت هر مقاله در آن گرایش یا حوزه ی علمی متناسب می باشد.
برخی از ویژگی های شبکه ی ارجاعات در زیر آمده است:
• جهت دار و بدون طوقه: در شبکه ی ارجاعات، که هر راس به معنی یک مقاله می باشد، اگر یالی از مقاله ای خارج و یه مقاله ی دوم وارد شده باشد، به معنی این است که مقاله ی اول یک ارجاع به مقاله ی دوم زده است. طبق این تعریف، در این گراف نمی تواند طوقه وجود داشته باشد چون یک مقاله نمی تواند به خودش ارجاع بزند.
• عموماً بدون دور: با توجه به این که وقتی یک مقاله به مقاله ی دومی ارجاع می زند، مقاله ی دوم چاپ شده است، پس نمی توانند دو یا چند مقاله هم زمان به هم ارجاع بزنند پس نمی توانیم به طور عمومی دور در گراف داشته باشیم. در این شبکه، در حالتی دور خواهیم داشت که پژوهش هایی که هم زمان در حال انجام هستند، پیش نویس های قبل از چاپ مقاله های هم دیگر را داشته باشند و از هم دیگر استفاده کنند و به هم ارجاع دهند. در این حالت خاص، می توانیم در این شبکه دور داشته باشیم.
• بی مقیاس و جهان کوچک: شبکه ی ارجاعات از نوع شبکه های بی مقیاس نیز هست یعنی تابع توزیع درجه راس های آن، توانی می باشد ( P ( k ) ∝ k − γ {\displaystyle P ( k ) \propto k^{ - \gamma }} ) . همچنین این شبکه، خاصیت جهان کوچکی را نیز دارد به این معنی که قطر گراف کوچک می باشد. [ ۱]
• هم سنخ جویی: شکبه های ارجاعات هم سنخ جو هستند یعنی راس هایی با درجه راس نزدیک به هم تمایل بیشتری به اتصال به هم را دارند.
• پودمانگی یا انجمنی: شبکه های ارجاعات خاصیت پودمانگی یا انجمنی دارند به این معنی که می توان آن ها را به صورت انجمن هایی دسته بندی کرد. برای مثال مقالات موجود در یک حوزه ی علمی، بیشتر به مقالات در همان حوزه ارجاع داده اند و کمتر به موضوعات خارج از آن حوزه.
• تابعیت زمانی و سازوکار اضافه و حذف راس: این گراف ها تابعیت زمانی دارند یعنی در طی زمان این گراف تغییر کرده و کامل تر می شود. با پیش رفتن زمان، راس های جدیدی به وجود آمده و یال های جدیدی به این گراف اضافه می شود. همچنین با اضافه شدن مقالات جدیدی که به مقالات قبلی ارجاع می زنند، درجه راس ورودی راس های از پیش موجود در گراف اضافه می شود. راس های دارای درجه راس ورودی بیشتر، احتمال گرفتن درجه راس ورودی بیشتری نیز دارند یعنی وقتی مقاله ی جدیدی منتشر می شود، با احتمال بیشتری به راس ها با درجه راس ورودی بیشتر ارجاع می زند. این سازوکار می تواند مانند مدل باراباسی - آلبرت مدل شود که به شبکه ای بی مقیاس منجر خواهد شد. همچنین در این شبکه حذف راس نداریم چون با گذر زمان قرار نیست ارجاعی حذف شود و فقط به یال ها و راس های این گراف اضافه می شود.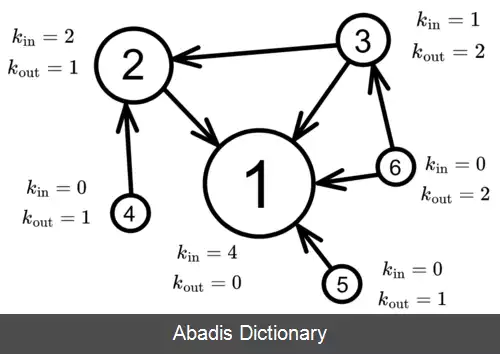



این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفشبکه های ارجاعات برای درک تأثیر مقالات و کارهای علمی در طول زمان بسیار مهم هستند. این شبکه ها، به محققان کمک می کنند مقالات کلیدی را در هر رشته و حوزه شناسایی کنند، توسعه ایده ها را ردیابی کنند و تأثیر تحقیقات را در درون و بین رشته ها اندازه گیری کنند.
اگر گراف ارجاعات را برای مقالات یک حوزه ی علمی رسم کنیم، با نگاه کردن به این شبکه و همچنین دیدن میزان یال هایی که به هر راس این گراف متصل هستند، می توان میزان اهمیت یک مقاله در آن حوزه را متوجه شد. میزان راس های ورودی با اهمیت هر مقاله در آن گرایش یا حوزه ی علمی متناسب می باشد.
برخی از ویژگی های شبکه ی ارجاعات در زیر آمده است:
• جهت دار و بدون طوقه: در شبکه ی ارجاعات، که هر راس به معنی یک مقاله می باشد، اگر یالی از مقاله ای خارج و یه مقاله ی دوم وارد شده باشد، به معنی این است که مقاله ی اول یک ارجاع به مقاله ی دوم زده است. طبق این تعریف، در این گراف نمی تواند طوقه وجود داشته باشد چون یک مقاله نمی تواند به خودش ارجاع بزند.
• عموماً بدون دور: با توجه به این که وقتی یک مقاله به مقاله ی دومی ارجاع می زند، مقاله ی دوم چاپ شده است، پس نمی توانند دو یا چند مقاله هم زمان به هم ارجاع بزنند پس نمی توانیم به طور عمومی دور در گراف داشته باشیم. در این شبکه، در حالتی دور خواهیم داشت که پژوهش هایی که هم زمان در حال انجام هستند، پیش نویس های قبل از چاپ مقاله های هم دیگر را داشته باشند و از هم دیگر استفاده کنند و به هم ارجاع دهند. در این حالت خاص، می توانیم در این شبکه دور داشته باشیم.
• بی مقیاس و جهان کوچک: شبکه ی ارجاعات از نوع شبکه های بی مقیاس نیز هست یعنی تابع توزیع درجه راس های آن، توانی می باشد ( P ( k ) ∝ k − γ {\displaystyle P ( k ) \propto k^{ - \gamma }} ) . همچنین این شبکه، خاصیت جهان کوچکی را نیز دارد به این معنی که قطر گراف کوچک می باشد. [ ۱]
• هم سنخ جویی: شکبه های ارجاعات هم سنخ جو هستند یعنی راس هایی با درجه راس نزدیک به هم تمایل بیشتری به اتصال به هم را دارند.
• پودمانگی یا انجمنی: شبکه های ارجاعات خاصیت پودمانگی یا انجمنی دارند به این معنی که می توان آن ها را به صورت انجمن هایی دسته بندی کرد. برای مثال مقالات موجود در یک حوزه ی علمی، بیشتر به مقالات در همان حوزه ارجاع داده اند و کمتر به موضوعات خارج از آن حوزه.
• تابعیت زمانی و سازوکار اضافه و حذف راس: این گراف ها تابعیت زمانی دارند یعنی در طی زمان این گراف تغییر کرده و کامل تر می شود. با پیش رفتن زمان، راس های جدیدی به وجود آمده و یال های جدیدی به این گراف اضافه می شود. همچنین با اضافه شدن مقالات جدیدی که به مقالات قبلی ارجاع می زنند، درجه راس ورودی راس های از پیش موجود در گراف اضافه می شود. راس های دارای درجه راس ورودی بیشتر، احتمال گرفتن درجه راس ورودی بیشتری نیز دارند یعنی وقتی مقاله ی جدیدی منتشر می شود، با احتمال بیشتری به راس ها با درجه راس ورودی بیشتر ارجاع می زند. این سازوکار می تواند مانند مدل باراباسی - آلبرت مدل شود که به شبکه ای بی مقیاس منجر خواهد شد. همچنین در این شبکه حذف راس نداریم چون با گذر زمان قرار نیست ارجاعی حذف شود و فقط به یال ها و راس های این گراف اضافه می شود.




wiki: شبکه ی ارجاعات
