شبکه مرتب سازی یک مدل انتزاعی ریاضی شامل شبکه ای از سیم ها و واحدهای مقایسه کننده است که برای مرتب سازی رشته ای از اعداد از آن استفاده می شود. هر مقایسه کننده دو سیم را به هم متصل می کند و مقادیر را با قرار دادن مقدار کوچکتر به یکی از سیم ها و مقدار بزرگتر به سیم دیگر، مرتب می کند. اصلی ترین تفاوت میان شبکه مرتب سازی و الگوریتم مرتب سازی این است که ترتیب مقایسه ها بدون در نظر گرفتن نتیجه مقایسه های قبلی، از قبل مشخص شده است. استقلال میان ترتیب مقایسه ها برای اجرای موازی الگوریتم ها مفید خواهد بود. علی رغم سادگی مدل آن، تئوری مرتب سازی شبکه ای بسیار پیچیده و دارای مفاهیم عمیقی است.
یک شبکه مرتب سازی شامل دو عنصر است، مقایسه کننده ها و سیم ها. هر سیم دارای یک مقدار می باشد، و هر مقایسه کننده دو سیم را به عنوان ورودی و خروجی می گیرد. زمانی که دو مقدار وارد مقایسه کننده می شود، مقایسه کننده مقدار کوچکتر را در سیم بالاتر، و مقدار بزرگتر را در سیم پایین قرار می دهد. به شبکه ای از سیم ها و مقایسه کننده ها که به طور صحیح تمام مقادیر ورودی را به صورت صعودی مرتب کنند یک شبکه مرتب سازی گفته می شود. مراحل انجام یک مرتب سازی شبکه ای ساده در شکل زیر نشان داده شده است. فهم چگونگی صحیح عمل نمودن این شبکه مرتب سازی آسان است، این را مدنظر داشته باشید که مقایسه کننده ها مقدار بزرگ را به سیم پایین و مقدار کوچک را به سیم بالا منتقل می کنند؛ و در نهایت آخرین مقایسه کننده دو سیم میانی را مرتب می کند.
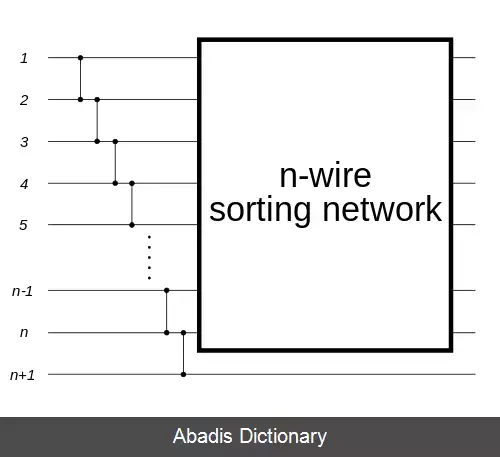
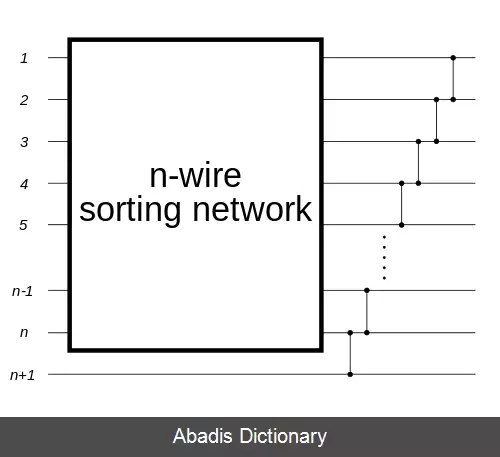
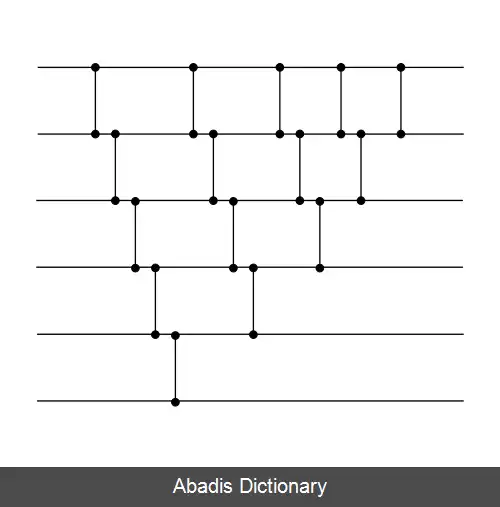
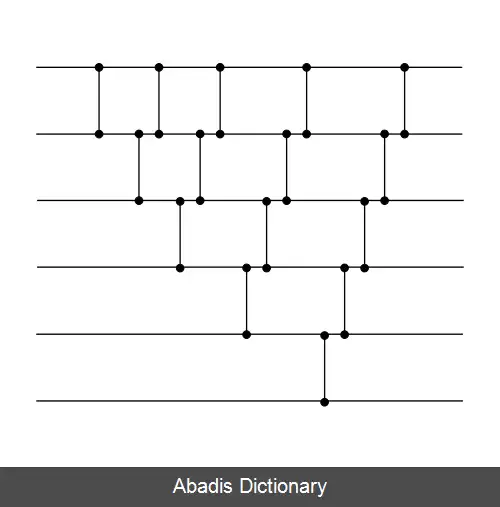
به راحتی می توان با استفاده از اصول درجی و انتخابی به صورت بازگشتی یک شبکه با اندازه دلخواه ایجاد کرد. با فرض این که یک شبکه مرتب سازی با اندازه n داریم، می توانیم با درج یک عدد اضافی به زیر شبکه مرتب شده ( با استفاده از اصول مرتب سازی درجی ) ، یک شبکه مرتب سازی با اندازه n+۱ بسازیم. همین کار را می توانیم به شکل دیگری انجام دهیم، ابتدا کوچکترین مقدار ورودی ها را انتخاب می کنیم، سپس مقادیر باقی مانده را به صورت بازگشتی مرتب می کنیم ( با استفاده از اصول مرتب سازی حبابی ) .
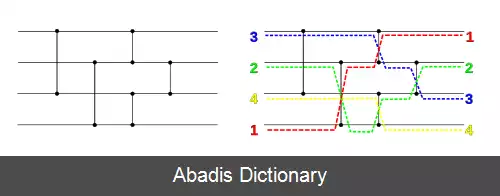
ساختار این دو مرتب سازی شبکه ای بسیار شبیه یکدیگر است، با نمایش هم زمان روند انجام مقایسه ها توسط مقایسه کننده ها عملاً می توان گفت که این دو یکی هستند.
شبکه درجی عمقی، به اندازه ( O ( n دارد، بنابراین استفاده از آن در عمل به صرفه نیست. شبکه های ساده ای وجود دارند با عمق O ( log n ) 2 و اندازه O ( n ( log n ) 2 ) ، مانند مرتب سازی ادغامی دسته ای فرد - زوج، مرتب سازی بایتونیک، و مرتب سازی صدفی. در عمل از این شبکه ها استفاده می شود.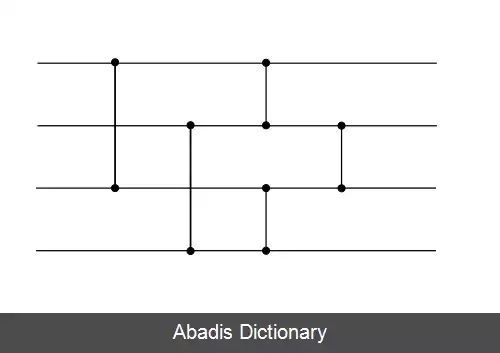
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک شبکه مرتب سازی شامل دو عنصر است، مقایسه کننده ها و سیم ها. هر سیم دارای یک مقدار می باشد، و هر مقایسه کننده دو سیم را به عنوان ورودی و خروجی می گیرد. زمانی که دو مقدار وارد مقایسه کننده می شود، مقایسه کننده مقدار کوچکتر را در سیم بالاتر، و مقدار بزرگتر را در سیم پایین قرار می دهد. به شبکه ای از سیم ها و مقایسه کننده ها که به طور صحیح تمام مقادیر ورودی را به صورت صعودی مرتب کنند یک شبکه مرتب سازی گفته می شود. مراحل انجام یک مرتب سازی شبکه ای ساده در شکل زیر نشان داده شده است. فهم چگونگی صحیح عمل نمودن این شبکه مرتب سازی آسان است، این را مدنظر داشته باشید که مقایسه کننده ها مقدار بزرگ را به سیم پایین و مقدار کوچک را به سیم بالا منتقل می کنند؛ و در نهایت آخرین مقایسه کننده دو سیم میانی را مرتب می کند.
به راحتی می توان با استفاده از اصول درجی و انتخابی به صورت بازگشتی یک شبکه با اندازه دلخواه ایجاد کرد. با فرض این که یک شبکه مرتب سازی با اندازه n داریم، می توانیم با درج یک عدد اضافی به زیر شبکه مرتب شده ( با استفاده از اصول مرتب سازی درجی ) ، یک شبکه مرتب سازی با اندازه n+۱ بسازیم. همین کار را می توانیم به شکل دیگری انجام دهیم، ابتدا کوچکترین مقدار ورودی ها را انتخاب می کنیم، سپس مقادیر باقی مانده را به صورت بازگشتی مرتب می کنیم ( با استفاده از اصول مرتب سازی حبابی ) .
ساختار این دو مرتب سازی شبکه ای بسیار شبیه یکدیگر است، با نمایش هم زمان روند انجام مقایسه ها توسط مقایسه کننده ها عملاً می توان گفت که این دو یکی هستند.
شبکه درجی عمقی، به اندازه ( O ( n دارد، بنابراین استفاده از آن در عمل به صرفه نیست. شبکه های ساده ای وجود دارند با عمق O ( log n ) 2 و اندازه O ( n ( log n ) 2 ) ، مانند مرتب سازی ادغامی دسته ای فرد - زوج، مرتب سازی بایتونیک، و مرتب سازی صدفی. در عمل از این شبکه ها استفاده می شود.






wiki: شبکه مرتب سازی
