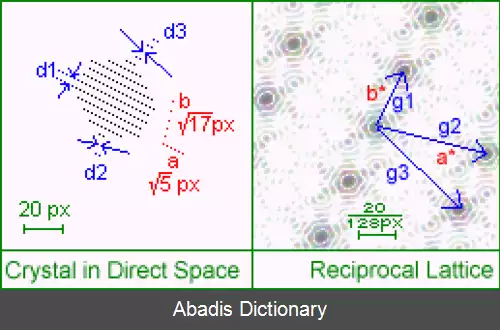
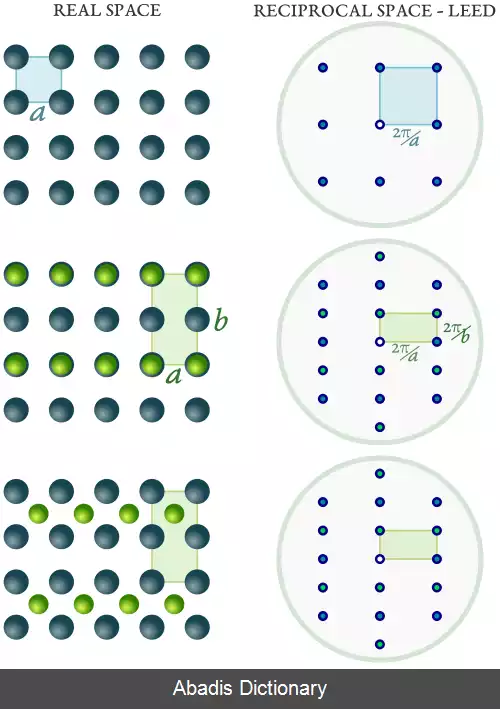
در فیزیک، شبکه متقابل نشان دهنده تبدیل فوریه یک شبکه ( گروه ) دیگر ( معمولاً یک شبکه براوه ) است. در استفاده معمولی، شبکه اولیه ( که تبدیل آن با شبکه متقابل نشان داده می شود ) یک تابع فضایی تناوبی در فضای واقعی است که به عنوان شبکه مستقیم شناخته می شود. در حالی که شبکه مستقیم در فضای واقعی وجود دارد و معمولاً به عنوان یک شبکه فیزیکی شناخته می شود ( مانند شبکه یک کریستال ) ، شبکه متقابل در فضای فرکانس های فضایی وجود دارد که به عنوان فضای متقابل یا فضای k شناخته می شود. k به بردار موج اشاره دارد. در فیزیک کوانتومی، فضای متقابل با توجه به تناسب p = ℏ k ارتباط نزدیکی با فضای تکانه دارد. جایی که p بردار حرکت است و ℏ ثابت پلانک است. شبکه متقابل یک شبکه متقابل معادل شبکه مستقیم اصلی است، زیرا معادلات تعیین کننده با توجه به بردارهای فضای واقعی و متقابل متقارن هستند. از نظر ریاضی، بردارهای شبکه مستقیم و متقابل به ترتیب بردارهای کوواریانت و متضاد را نشان می دهند.
شبکه متقابل مجموعه ای از تمام بردارها است {\displaystyle \mathbf {G} _{m}}، که بردارهای موج های مسطح در سری فوریه تابع فضایی هستند که تناوب آن با شبکه مستقیم یکسان است. < math> \mathbf{R}_n< /math> . هر موج مسطح در این سری فوریه فاز یا فازهای یکسانی دارد که مضربی از آنها متفاوت است{{nowrap begin}}< math> 2\pi< /math> {{nowrap end}} در هر نقطه شبکه مستقیم ( بنابراین اساساً فاز یکسان در تمام نقاط شبکه مستقیم ) .
شبکه متقابل نقش اساسی در بیشتر مطالعات تحلیلی ساختارهای تناوبی، به ویژه در تئوری پراش دارد. در پراش نوترون، هلیوم و اشعه ایکس، به دلیل شرایط لائو، تفاوت تکانه بین پرتوهای ایکس ورودی و پراش یک کریستال یک بردار شبکه متقابل است. از الگوی پراش یک کریستال می توان برای تعیین بردارهای متقابل شبکه استفاده کرد. با استفاده از این فرایند، می توان آرایش اتمی یک کریستال را استنباط کرد.
منطقه بریلوین یک سلول ویگنر - سیتس از شبکه متقابل است.
فضای متقابل ( که k - space نیز نامیده می شود ) راهی برای تجسم نتایج تبدیل فوریه یک تابع فضایی فراهم می کند. از نظر نقش شبیه به حوزه فرکانس ناشی از تبدیل فوریه یک تابع وابسته به زمان است. فضای متقابل فضایی است که بر روی آن تبدیل فوریه یک تابع فضایی در فرکانس های فضایی یا بردار موج امواج صفحه تبدیل فوریه نشان داده می شود. دامنه خود تابع فضایی اغلب به عنوان فضای واقعی نامیده می شود. در کاربردهای فیزیکی، مانند کریستالوگرافی، هر دو فضای واقعی و متقابل اغلب دو یا سه بعدی هستند. در حالی که ابعاد فضایی این دو فضای مرتبط یکسان خواهد بود، فضاها در واحدهای طول خود متفاوت خواهند بود، به طوری که وقتی فضای واقعی دارای واحدهای طول L باشد، فضای متقابل آن دارای واحدهای یک تقسیم بر طول L یا معکوس L خواهد بود. ( مقابل طول ) .
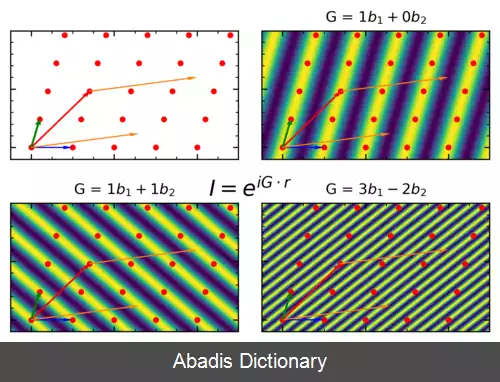

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفشبکه متقابل مجموعه ای از تمام بردارها است {\displaystyle \mathbf {G} _{m}}، که بردارهای موج های مسطح در سری فوریه تابع فضایی هستند که تناوب آن با شبکه مستقیم یکسان است. < math> \mathbf{R}_n< /math> . هر موج مسطح در این سری فوریه فاز یا فازهای یکسانی دارد که مضربی از آنها متفاوت است{{nowrap begin}}< math> 2\pi< /math> {{nowrap end}} در هر نقطه شبکه مستقیم ( بنابراین اساساً فاز یکسان در تمام نقاط شبکه مستقیم ) .
شبکه متقابل نقش اساسی در بیشتر مطالعات تحلیلی ساختارهای تناوبی، به ویژه در تئوری پراش دارد. در پراش نوترون، هلیوم و اشعه ایکس، به دلیل شرایط لائو، تفاوت تکانه بین پرتوهای ایکس ورودی و پراش یک کریستال یک بردار شبکه متقابل است. از الگوی پراش یک کریستال می توان برای تعیین بردارهای متقابل شبکه استفاده کرد. با استفاده از این فرایند، می توان آرایش اتمی یک کریستال را استنباط کرد.
منطقه بریلوین یک سلول ویگنر - سیتس از شبکه متقابل است.
فضای متقابل ( که k - space نیز نامیده می شود ) راهی برای تجسم نتایج تبدیل فوریه یک تابع فضایی فراهم می کند. از نظر نقش شبیه به حوزه فرکانس ناشی از تبدیل فوریه یک تابع وابسته به زمان است. فضای متقابل فضایی است که بر روی آن تبدیل فوریه یک تابع فضایی در فرکانس های فضایی یا بردار موج امواج صفحه تبدیل فوریه نشان داده می شود. دامنه خود تابع فضایی اغلب به عنوان فضای واقعی نامیده می شود. در کاربردهای فیزیکی، مانند کریستالوگرافی، هر دو فضای واقعی و متقابل اغلب دو یا سه بعدی هستند. در حالی که ابعاد فضایی این دو فضای مرتبط یکسان خواهد بود، فضاها در واحدهای طول خود متفاوت خواهند بود، به طوری که وقتی فضای واقعی دارای واحدهای طول L باشد، فضای متقابل آن دارای واحدهای یک تقسیم بر طول L یا معکوس L خواهد بود. ( مقابل طول ) .





wiki: شبکه متقابل
