در هندسهٔ تحلیلی، سطح مخروطی یا رویهٔ مخروطی ( به انگلیسی: Conical surface ) یک رویهٔ بی کران است که از دوران یک خط حول یک محور ( متقاطع ) به دست می آید.
به طور کلّی تر، یک مخروط بیضوی ( به انگلیسی: Elliptic Cone ) از انواع رویه های درجهٔ دوم است. [ ۱]
به مخروط بیضوی و نیز به سطح مخروطی، به طور خلاصه مخروط نیز می گویند. در گذشته «مخروط» به معنی سطحی کران دار و قائم با قاعدهٔ دایره بود. در طی زمان ها مفهوم کلمهٔ «مخروط» مخروط اریب را نیز شامل شد و پس از پیشرفت بیشتر ریاضیات، این اصطلاح کامل تر شد و سطح مخروطی را نیز شامل شد. هنوز در تدریس ریاضی در سطوح ابتدایی در جهان از معنی قدیمی استفاده می شود. [ ۲]
هر سطح مخروطی سه محور ( خط ) تقارن عمود برهم دارد که در یک مرکز ( نقطه ) تقارن با یکدیگر تقاطع دارند.
به مرکز تقارن سطح مخروطی رأس آن می گویند و به محور تقارن آن محور. هر خط روی مخروط ( خطوطی که با دوران آن ها حول محور، مخروط به دست می آید ) را یک مولّد سطح مخروطی می نامند. [ ۳]
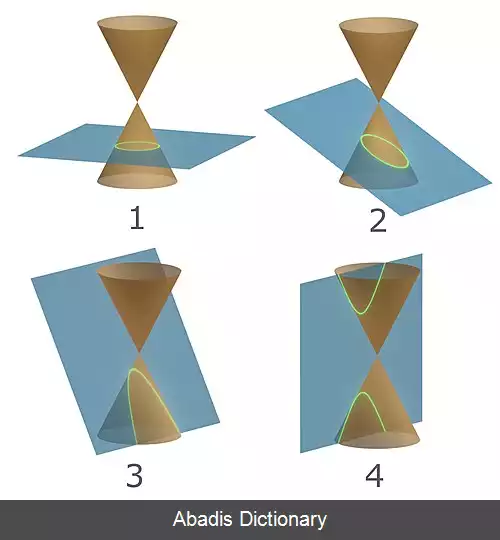
هر سطح مقطع از سطح مخروطی یا یک هذلولی ست، یا سهمی، یا بیضی یا دایره، یا یک خط یا نقطه یا تهی ست. [ ۳]
در دستگاه مختصات دکارتی، روش استاندارد نمایش یک مخروط بیضوی با مرکز تقارن در مبدأ مختصات به صورت زیر است:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = 0
اگر a = b باشد سطح مخروطی ( دایروی ) حاصل می شود.
یک ابرمخروط در فضای R n ، یک ابررویهٔ درجه دو است. یک ابرمخروط، همهٔ نقاطی مانند P = ( x 1 , x 2 , … , x n ) است که در معادلهٔ استاندارد زیر صدق کنند:
± x 1 2 c 1 2 ± x 2 2 c 2 2 ± ⋯ ± x n 2 c n 2 = 0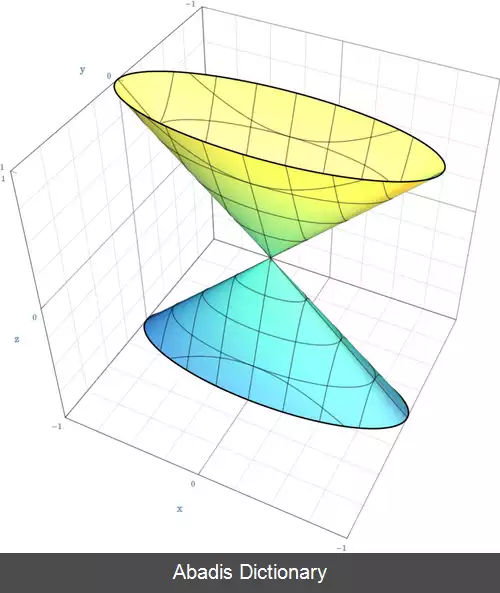
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور کلّی تر، یک مخروط بیضوی ( به انگلیسی: Elliptic Cone ) از انواع رویه های درجهٔ دوم است. [ ۱]
به مخروط بیضوی و نیز به سطح مخروطی، به طور خلاصه مخروط نیز می گویند. در گذشته «مخروط» به معنی سطحی کران دار و قائم با قاعدهٔ دایره بود. در طی زمان ها مفهوم کلمهٔ «مخروط» مخروط اریب را نیز شامل شد و پس از پیشرفت بیشتر ریاضیات، این اصطلاح کامل تر شد و سطح مخروطی را نیز شامل شد. هنوز در تدریس ریاضی در سطوح ابتدایی در جهان از معنی قدیمی استفاده می شود. [ ۲]
هر سطح مخروطی سه محور ( خط ) تقارن عمود برهم دارد که در یک مرکز ( نقطه ) تقارن با یکدیگر تقاطع دارند.
به مرکز تقارن سطح مخروطی رأس آن می گویند و به محور تقارن آن محور. هر خط روی مخروط ( خطوطی که با دوران آن ها حول محور، مخروط به دست می آید ) را یک مولّد سطح مخروطی می نامند. [ ۳]
هر سطح مقطع از سطح مخروطی یا یک هذلولی ست، یا سهمی، یا بیضی یا دایره، یا یک خط یا نقطه یا تهی ست. [ ۳]
در دستگاه مختصات دکارتی، روش استاندارد نمایش یک مخروط بیضوی با مرکز تقارن در مبدأ مختصات به صورت زیر است:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = 0
اگر a = b باشد سطح مخروطی ( دایروی ) حاصل می شود.
یک ابرمخروط در فضای R n ، یک ابررویهٔ درجه دو است. یک ابرمخروط، همهٔ نقاطی مانند P = ( x 1 , x 2 , … , x n ) است که در معادلهٔ استاندارد زیر صدق کنند:
± x 1 2 c 1 2 ± x 2 2 c 2 2 ± ⋯ ± x n 2 c n 2 = 0


wiki: سطح مخروطی
