در ریاضیات، سری هندسی به دنباله ای از اعداد می گویند که هر جمله آن، ضرب یک عدد ثابت بنام قدر نسبت در جمله قبلی باشد که در آن جمله اول هر عددی می تواند باشد، در اینصورت مجموع سری یک تصاعد هندسی به صورت زیر تعریف می شود:
در این سری، a را جمله اول و r را قدر نسبت سری می نامند.
باید توجه کرد که هر سری، خود یک دنباله است و توسط دنباله دیگری بنام دنباله مولد سری مذکور، با قانون خاصی که نوع سری را مشخص می کند، به دست می آید و نباید سری را با مجموع آن سری اشتباه کرد و این اشتباه درباره سری ها بصورت چشمگیری مشاهده می شود.
برای نمونه مجموع زیر یک سری هندسی با قدر نسبت ۱/۲ است.
در سری هندسی اگر r < 1 باشد این سری همگرا خواهد بود. در غیر این صورت این سری واگرا است.
مجموع یک سری هندسی همگرا ( r < 1 ) از رابطه زیر به دست می آید:
• موقعی که | r | = 1 {\displaystyle |r|\; =\ 1} سری تبدیل می شود به:
مجموع این سری می شود:
و
( علامت بستگی به منفی یا مثبت بودن a دارد ) .
این واگرائی سری را نشان می دهد.
اکنون اگر r = − 1 سری تبدیل می شود به:
بنابراین دنباله مجموع آن به شکل زیر در می آید:
که واگرا می باشد.
• حالا ملاحظه کنید موقعی که قدر نسبت سری | r | ≠ 1 {\displaystyle |r|\; \neq \ 1} .
( ١ ) S n = a + a r + a r 2 + . . . + a r n
هر دو طرف معادله را با r ضرب می کنیم:
( ٢ ) r S n = a r + a r 2 + . . . + a r n + a r n + 1
( ٢ ) را از ( ١ ) کم می کنیم:
( ٣ ) S n − r S n = a − a r n + 1
یا:
( 1 − r ) S n = a − a r n + 1
از آنجائی که در وضعیت مورد نظر | r | ≠ 1 ، ما می توانیم آن را به شکل زیر بنویسیم:
اگر r < 1 پس l i m n → ∞ r n + 1 = 0 و نتیجه می گیریم که سری همگرا است.
یک سری با قدر نسبت r = 1 2 را در نظر بگیرید:
از آنجا که قدر نسبت کوچکتر از یک است این سری همگرا است. همگرایی این سری نیز به سمت 1 است.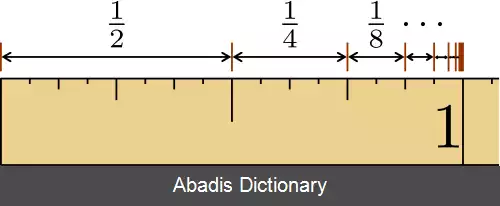
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این سری، a را جمله اول و r را قدر نسبت سری می نامند.
باید توجه کرد که هر سری، خود یک دنباله است و توسط دنباله دیگری بنام دنباله مولد سری مذکور، با قانون خاصی که نوع سری را مشخص می کند، به دست می آید و نباید سری را با مجموع آن سری اشتباه کرد و این اشتباه درباره سری ها بصورت چشمگیری مشاهده می شود.
برای نمونه مجموع زیر یک سری هندسی با قدر نسبت ۱/۲ است.
در سری هندسی اگر r < 1 باشد این سری همگرا خواهد بود. در غیر این صورت این سری واگرا است.
مجموع یک سری هندسی همگرا ( r < 1 ) از رابطه زیر به دست می آید:
• موقعی که | r | = 1 {\displaystyle |r|\; =\ 1} سری تبدیل می شود به:
مجموع این سری می شود:
و
( علامت بستگی به منفی یا مثبت بودن a دارد ) .
این واگرائی سری را نشان می دهد.
اکنون اگر r = − 1 سری تبدیل می شود به:
بنابراین دنباله مجموع آن به شکل زیر در می آید:
که واگرا می باشد.
• حالا ملاحظه کنید موقعی که قدر نسبت سری | r | ≠ 1 {\displaystyle |r|\; \neq \ 1} .
( ١ ) S n = a + a r + a r 2 + . . . + a r n
هر دو طرف معادله را با r ضرب می کنیم:
( ٢ ) r S n = a r + a r 2 + . . . + a r n + a r n + 1
( ٢ ) را از ( ١ ) کم می کنیم:
( ٣ ) S n − r S n = a − a r n + 1
یا:
( 1 − r ) S n = a − a r n + 1
از آنجائی که در وضعیت مورد نظر | r | ≠ 1 ، ما می توانیم آن را به شکل زیر بنویسیم:
اگر r < 1 پس l i m n → ∞ r n + 1 = 0 و نتیجه می گیریم که سری همگرا است.
یک سری با قدر نسبت r = 1 2 را در نظر بگیرید:
از آنجا که قدر نسبت کوچکتر از یک است این سری همگرا است. همگرایی این سری نیز به سمت 1 است.

wiki: سری هندسی
