سرعت نسبی
فرهنگستان زبان و ادب
دانشنامه عمومی
سرعت نسبی v → B ∣ A ( همچنین v → B A یا v → B rel A ) سرعت یک شی یا مشاهده گر B در بقیه چارچوب از یک شی دیگر یا ناظر A است.
ما با حرکت نسبی در تقریب کلاسیک ( یا غیر نسبی، یا تقریب نیوتنی ) شروع می کنیم که همه سرعت ها بسیار کمتر از سرعت نور است. این با تبدیل های گالیله همراه است. تصویر یک مرد را در بالای قطار نشان می دهد. در ساعت ۱:۰۰ بعد از ظهر شروع به قدم زدن با سرعت ۱۰ کیلومتر / ساعت می کند. قطار هم در حال حرکت با سرعت ۴۰ کیلومتر / ساعت است. تصویر مرد و قطار را در دو زمان نشان می دهد: اول، زمانی که سفر آغاز شده است، و یک ساعت بعد در ساعت ۲ بعد از ظهر. تصویر نشان می دهد که مرد ۵۰ کیلومتر از نقطه شروع فاصله دارد چون یک ساعت با قطار و خودش حرکت کرده اند. این، طبق تعریف، سرعت ۵۰ کیلومتر / ساعت، که نشان می دهد که روش محاسبه سرعت نسبی در این حالت، جمع دو سرعت است.
تصویر ساعت ها و خط کش به خواننده یادآوری می کند که در حالی که منطق پشت این محاسبات بی عیب و نقص به نظر می رسد، پیش فرض های اشتباه در مورد چگونگی رفتار ساعت ها و خط کش دارد. ( آزمایش قطار و پلت فرم را ببینید. ) به رسمیت شناختن این مدل کلاسیک از حرکت نسبی نقض نسبیت خاص است، ما مثال را به یک معادله تعمیم می دهیم:
که:
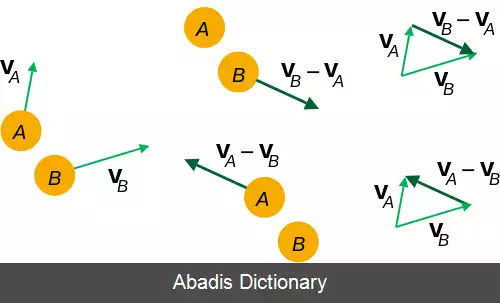
شکل دو شی A و B که با سرعت ثابت حرکت می کنند را نشان می هد. معادلات حرکت عبارتند از:
که زیرنویس i اشاره به جابجایی اولیه ( در زمان t برابر با صفر ) است. تفاوت بین دو بردار جابه جایی، r → B − r → A ، نشان دهنده محل B از دید A می باشد.
از این رو:
پس از جایگذاری v → A | C = v → A and v → B | C = v → B ، ما داریم:
برای ساخت نظریه حرکت نسبی سازگار با نظریه نسبیت خاص، ما باید یک قاعده متفاوت اتخاذ کنیم. برای ادامه کار در محدودهٔ نیوتنی ( غیر نسبی ) ، ما با یک تبدیل گالیله در یک بعد شروع می کنیم:
که در آن x 'موقعیت است که توسط یک چارچوب مرجع که با سرعت، v در چارچوب مرجع «پرایم دار» ( x ) حرکت می کند دیده می شود. با مشتق گرفتن از دو معادله فوق، ما، d x ′ = d x − v d t و آنچه که ممکن است به عنوان بدیهی مشهود باشد d t ′ = d t بدست می آوریم، داریم:
برای بازیابی عبارات قبلی برای سرعت نسبی، فرض می کنیم که ذره A مسیری را که توسط dx / dt تعریف شده در مرجع بدون پرایم ( و در نتیجه dx ′ / dt ′ در چارچوب پرایم دار ) دنبال می شود. بدین ترتیب d x / d t = v A ∣ O و d x ′ / d t = v A ∣ O ′ ، جایی که O و O ′ اشاره به حرکت A از دید به ترتیب چارچوب بدون پرایم و با پرایم است. به یاد بیاورید که v یک حرکت ثابت در چارچوب پرایم دار شده است، همان طور که از چارچوب بدون پرایم دیده می شود؛ بنابراین ما داریم v = v O ′ ∣ O ، و: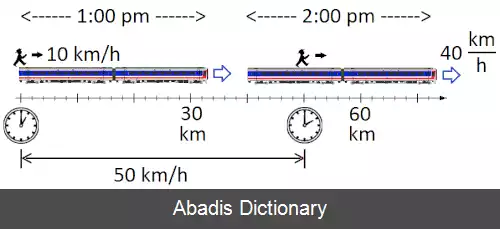
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفما با حرکت نسبی در تقریب کلاسیک ( یا غیر نسبی، یا تقریب نیوتنی ) شروع می کنیم که همه سرعت ها بسیار کمتر از سرعت نور است. این با تبدیل های گالیله همراه است. تصویر یک مرد را در بالای قطار نشان می دهد. در ساعت ۱:۰۰ بعد از ظهر شروع به قدم زدن با سرعت ۱۰ کیلومتر / ساعت می کند. قطار هم در حال حرکت با سرعت ۴۰ کیلومتر / ساعت است. تصویر مرد و قطار را در دو زمان نشان می دهد: اول، زمانی که سفر آغاز شده است، و یک ساعت بعد در ساعت ۲ بعد از ظهر. تصویر نشان می دهد که مرد ۵۰ کیلومتر از نقطه شروع فاصله دارد چون یک ساعت با قطار و خودش حرکت کرده اند. این، طبق تعریف، سرعت ۵۰ کیلومتر / ساعت، که نشان می دهد که روش محاسبه سرعت نسبی در این حالت، جمع دو سرعت است.
تصویر ساعت ها و خط کش به خواننده یادآوری می کند که در حالی که منطق پشت این محاسبات بی عیب و نقص به نظر می رسد، پیش فرض های اشتباه در مورد چگونگی رفتار ساعت ها و خط کش دارد. ( آزمایش قطار و پلت فرم را ببینید. ) به رسمیت شناختن این مدل کلاسیک از حرکت نسبی نقض نسبیت خاص است، ما مثال را به یک معادله تعمیم می دهیم:
که:
شکل دو شی A و B که با سرعت ثابت حرکت می کنند را نشان می هد. معادلات حرکت عبارتند از:
که زیرنویس i اشاره به جابجایی اولیه ( در زمان t برابر با صفر ) است. تفاوت بین دو بردار جابه جایی، r → B − r → A ، نشان دهنده محل B از دید A می باشد.
از این رو:
پس از جایگذاری v → A | C = v → A and v → B | C = v → B ، ما داریم:
برای ساخت نظریه حرکت نسبی سازگار با نظریه نسبیت خاص، ما باید یک قاعده متفاوت اتخاذ کنیم. برای ادامه کار در محدودهٔ نیوتنی ( غیر نسبی ) ، ما با یک تبدیل گالیله در یک بعد شروع می کنیم:
که در آن x 'موقعیت است که توسط یک چارچوب مرجع که با سرعت، v در چارچوب مرجع «پرایم دار» ( x ) حرکت می کند دیده می شود. با مشتق گرفتن از دو معادله فوق، ما، d x ′ = d x − v d t و آنچه که ممکن است به عنوان بدیهی مشهود باشد d t ′ = d t بدست می آوریم، داریم:
برای بازیابی عبارات قبلی برای سرعت نسبی، فرض می کنیم که ذره A مسیری را که توسط dx / dt تعریف شده در مرجع بدون پرایم ( و در نتیجه dx ′ / dt ′ در چارچوب پرایم دار ) دنبال می شود. بدین ترتیب d x / d t = v A ∣ O و d x ′ / d t = v A ∣ O ′ ، جایی که O و O ′ اشاره به حرکت A از دید به ترتیب چارچوب بدون پرایم و با پرایم است. به یاد بیاورید که v یک حرکت ثابت در چارچوب پرایم دار شده است، همان طور که از چارچوب بدون پرایم دیده می شود؛ بنابراین ما داریم v = v O ′ ∣ O ، و:


wiki: سرعت نسبی
پیشنهاد کاربران
هنگار ناپایدار، هنگار دگرش پذیر
