ساخت با خط کش و پرگار ( به انگلیسی: Straightedge and Compass Construction ) ( یا Ruler - and - Compass Construction ) ( یا ترسیم با خط کش و پرگار یا ساخت کلاسیک ) ، به ساخت طول ها، زوایا، و سایر اشکال هندسی با استفاده از خطکش و پرگار ایده آل گفته می شود.
خط کش و پرگار تنها ابزارهای مجاز ترسیم در هندسه اقلیدسی هستند، [ ۱] تا جایی که هندسهٔ اقلیدسی گاه «هندسهٔ خط کش و پرگار» خوانده شده است. [ ۲] پرگار ابزاری برای کشیدن دایره بر اساس تعریف اقلیدسی آن است[ ۳] و با خط کشی با طول بی نهایت می توان خط راست کشید، و هدف ریاضی دانان اقلیدسی این بود که همهٔ اشکال را با این دو ابزار بسازند. [ ۴] بنابراین در ترسیم با خط کش و پرگار تنها از سه اصل اول اصول موضوعه هندسه اقلیدسی می توان استفاده کرد. بنابر اثبات گاوس، تنها شکل هایی را می توان با خط کش و پرگار رسم کرد که اندازه شان عدد ترسیم پذیر باشد. اعداد ترسیم پذیر اعدادی اند که بتوان آن ها را با اعمال چهار عمل اصلی و ریشه دوم بر یک عدد ترسیم پذیر دیگر به دست آورد ( صفر و یک بنابر تعریف ترسیم پذیرند ) .
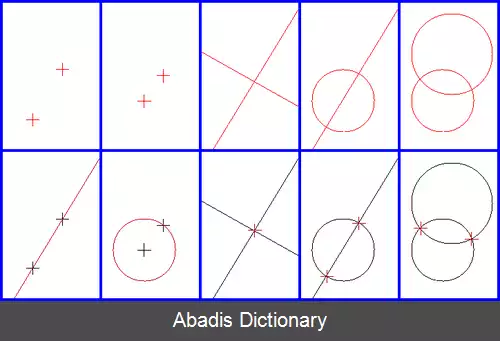
همهٔ ترسیم ها با خط کش و پرگار با تکرار و ترکیب پنج ترسیم بنیادی در صفحه صورت می گیرند. این پنج ترسیم بنیادی عبارتند از:
• ساخت یک خط با داشتن دو نقطه ( اصل اول از اصول موضوعه هندسه اقلیدسی )
• ساخت یک دایره با داشتن دو نقطه ( اصل سوم از اصول موضوعه هندسه اقلیدسی )
• ساخت یک نقطه در محل تقاطع دو خط ناموازی
• ساخت دو نقطه در محل تقاطع یک خط و یک دایره ( در صورت تقاطع )
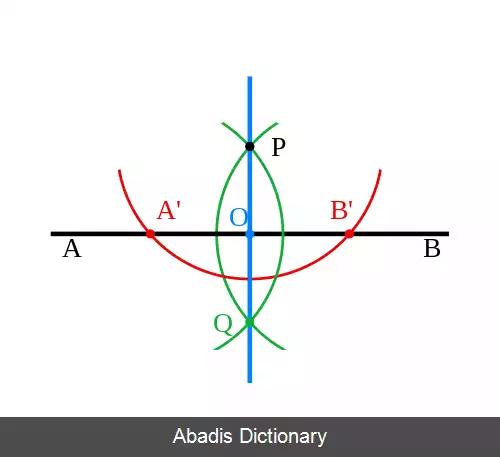
• ساخت دو نقطه در محل تقاطع دو دایره ( در صورت تقاطع )
تربیع دایره از مسائل کهن ریاضی است و هدف آن ترسیم مربعی با خط کش و پرگار است که مساحت آن با مساحت دایره ای مفروض برابر باشد. شکل دیگری از مسئله ترسیم مربعی با خط کش و پرگار است که محیط آن با محیط دایرهٔ مفروض برابر باشد. [ ۸] در ۱۸۸۲ فردیناند فون لیندمن نشان داد که پی عددی متعالی است، و تربیع دایره غیرممکن است. در زبان انگلیسی «تربیع دایره» ( به انگلیسی: squaring the circle ) وارد ادبیات شده است و همچنین ضرب المثلی به مفهوم «عمل غیرممکن» است. [ ۹]
تضعیف مکعب یا «مسئلهٔ دلوسی» نیز یکی مسائل کهن ریاضی است و هدفش ترسیم مکعبی با خط کش و پرگار است که حجم آن دو برابر حجم مکعبی مفروض باشد؛ به عبارت دیگر هر ضلع مکعب مطلوب باید 2 3 برابر ضلع مکعب مفروض باشد. [ ۱۰] پیر ونزل در ۱۸۳۷ نشان داد که این مسئله جوابی ندارد.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفخط کش و پرگار تنها ابزارهای مجاز ترسیم در هندسه اقلیدسی هستند، [ ۱] تا جایی که هندسهٔ اقلیدسی گاه «هندسهٔ خط کش و پرگار» خوانده شده است. [ ۲] پرگار ابزاری برای کشیدن دایره بر اساس تعریف اقلیدسی آن است[ ۳] و با خط کشی با طول بی نهایت می توان خط راست کشید، و هدف ریاضی دانان اقلیدسی این بود که همهٔ اشکال را با این دو ابزار بسازند. [ ۴] بنابراین در ترسیم با خط کش و پرگار تنها از سه اصل اول اصول موضوعه هندسه اقلیدسی می توان استفاده کرد. بنابر اثبات گاوس، تنها شکل هایی را می توان با خط کش و پرگار رسم کرد که اندازه شان عدد ترسیم پذیر باشد. اعداد ترسیم پذیر اعدادی اند که بتوان آن ها را با اعمال چهار عمل اصلی و ریشه دوم بر یک عدد ترسیم پذیر دیگر به دست آورد ( صفر و یک بنابر تعریف ترسیم پذیرند ) .
همهٔ ترسیم ها با خط کش و پرگار با تکرار و ترکیب پنج ترسیم بنیادی در صفحه صورت می گیرند. این پنج ترسیم بنیادی عبارتند از:
• ساخت یک خط با داشتن دو نقطه ( اصل اول از اصول موضوعه هندسه اقلیدسی )
• ساخت یک دایره با داشتن دو نقطه ( اصل سوم از اصول موضوعه هندسه اقلیدسی )
• ساخت یک نقطه در محل تقاطع دو خط ناموازی
• ساخت دو نقطه در محل تقاطع یک خط و یک دایره ( در صورت تقاطع )
• ساخت دو نقطه در محل تقاطع دو دایره ( در صورت تقاطع )
تربیع دایره از مسائل کهن ریاضی است و هدف آن ترسیم مربعی با خط کش و پرگار است که مساحت آن با مساحت دایره ای مفروض برابر باشد. شکل دیگری از مسئله ترسیم مربعی با خط کش و پرگار است که محیط آن با محیط دایرهٔ مفروض برابر باشد. [ ۸] در ۱۸۸۲ فردیناند فون لیندمن نشان داد که پی عددی متعالی است، و تربیع دایره غیرممکن است. در زبان انگلیسی «تربیع دایره» ( به انگلیسی: squaring the circle ) وارد ادبیات شده است و همچنین ضرب المثلی به مفهوم «عمل غیرممکن» است. [ ۹]
تضعیف مکعب یا «مسئلهٔ دلوسی» نیز یکی مسائل کهن ریاضی است و هدفش ترسیم مکعبی با خط کش و پرگار است که حجم آن دو برابر حجم مکعبی مفروض باشد؛ به عبارت دیگر هر ضلع مکعب مطلوب باید 2 3 برابر ضلع مکعب مفروض باشد. [ ۱۰] پیر ونزل در ۱۸۳۷ نشان داد که این مسئله جوابی ندارد.






wiki: ساخت با خط کش و پرگار
