در نظریه احتمالات زمان توقف ( به انگلیسی: stopping time ) که به آن زمان مارکوف ( به انگلیسی: Markov time ) هم می گویند یک متغیر تصادفی است و بیان گر زمان انجام یک فرایند تصادفی است. [ ۱]
یک پیشامد مشخصی را در نظر بگیرید که زمان وقوع آن را نمی دانیم ولی می دانیم این رخداد در یک زمان τ ای بالاخره رخ خواهد داد، زمان τ را زمان توقف می نامیم اگر در هر نقطه ای از زمان بدانیم پیشامد رخ داده است یا خیر.
به شرطی که با ارضا شدن آن شرط، توقف رخ خواهد داد شرط توقف می گویند. مثالی از شرط توقف در شکل رو به رو در حرکت براونی یک بعدی قابل مشاهده است.
محور زمان T ⊆ R + را در نظر بگیرید. اگر ( Ω , F , ( F t ) t ∈ T , P ) یک فضای احتمالاتی تصفیه شده باشد؛ که Ω فضای نمونه ای، F پیشامد و P توزیع احتمالاتی رخداد پیشامد باشد، داریم:
متغیر تصادفی τ → T ∪ { + ∞ } را زمان مارکوف تعریف می کنیم اگر:
∀ τ ∈ T : ( τ = T ) ∈ F t
که عبارت بالا مشابه عبارت زیر است. [ ۲]
∀ τ ∈ T : ( τ ≤ T ) ∈ F t
اگر ( Ω , F , ( F t ) t ∈ T , P ) یک فضای احتمالاتی تصفیه شده باشد. اگر در فضای احتمالی τ را متغیر تصادفی در نظر بگیریم به طوری که t ∈ T باشد. آنگاه τ برابر با زمان توقف است اگر و تنها اگر فرایند تصادفی X به صورت زیر باشد:
• خالی شدن حساب بانکی یک فرد ( شرط توقف است ) :
اگر τ را زمان خالی شدن حساب بانکی یک فرد در نظر بگیریم، با این که فرد نمی داند که کی حساب بانکی اش خالی می شود و آیا اصلاً حساب بانکی اش خالی خواهد شد، اما در هر زمانی فرد می داند که حسابش خالی است یا خیر؛ بنابراین τ را می توان یک زمان توقف در نظر گرفت.
• پیدا کردن نزدیک ترین جای پارک به سینما ( شرط توقف نیست ) :
فردی می خواهد خودرویش را در نزدیک ترین جای پارک به سینمایی که در انتهای یک خیابان قرار دارد، پارک کند. هنگامی که فرد از کنار یک جای پراک خالی عبور می کند می داند که از کنار یک جای پارک خالی عبور می کند، اما نمی داند که آیا این جای پارک نزدیک ترین جای پارک به سینما است یا جای پارک نزدیک تری هم به سینما وجود دارد؛ بنابراین این شرط نمی تواند یک شرط توقف باشد.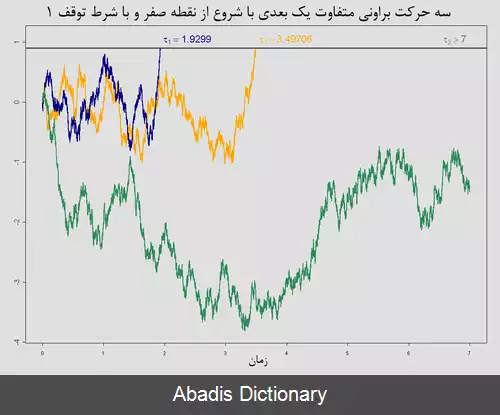
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک پیشامد مشخصی را در نظر بگیرید که زمان وقوع آن را نمی دانیم ولی می دانیم این رخداد در یک زمان τ ای بالاخره رخ خواهد داد، زمان τ را زمان توقف می نامیم اگر در هر نقطه ای از زمان بدانیم پیشامد رخ داده است یا خیر.
به شرطی که با ارضا شدن آن شرط، توقف رخ خواهد داد شرط توقف می گویند. مثالی از شرط توقف در شکل رو به رو در حرکت براونی یک بعدی قابل مشاهده است.
محور زمان T ⊆ R + را در نظر بگیرید. اگر ( Ω , F , ( F t ) t ∈ T , P ) یک فضای احتمالاتی تصفیه شده باشد؛ که Ω فضای نمونه ای، F پیشامد و P توزیع احتمالاتی رخداد پیشامد باشد، داریم:
متغیر تصادفی τ → T ∪ { + ∞ } را زمان مارکوف تعریف می کنیم اگر:
∀ τ ∈ T : ( τ = T ) ∈ F t
که عبارت بالا مشابه عبارت زیر است. [ ۲]
∀ τ ∈ T : ( τ ≤ T ) ∈ F t
اگر ( Ω , F , ( F t ) t ∈ T , P ) یک فضای احتمالاتی تصفیه شده باشد. اگر در فضای احتمالی τ را متغیر تصادفی در نظر بگیریم به طوری که t ∈ T باشد. آنگاه τ برابر با زمان توقف است اگر و تنها اگر فرایند تصادفی X به صورت زیر باشد:
• خالی شدن حساب بانکی یک فرد ( شرط توقف است ) :
اگر τ را زمان خالی شدن حساب بانکی یک فرد در نظر بگیریم، با این که فرد نمی داند که کی حساب بانکی اش خالی می شود و آیا اصلاً حساب بانکی اش خالی خواهد شد، اما در هر زمانی فرد می داند که حسابش خالی است یا خیر؛ بنابراین τ را می توان یک زمان توقف در نظر گرفت.
• پیدا کردن نزدیک ترین جای پارک به سینما ( شرط توقف نیست ) :
فردی می خواهد خودرویش را در نزدیک ترین جای پارک به سینمایی که در انتهای یک خیابان قرار دارد، پارک کند. هنگامی که فرد از کنار یک جای پراک خالی عبور می کند می داند که از کنار یک جای پارک خالی عبور می کند، اما نمی داند که آیا این جای پارک نزدیک ترین جای پارک به سینما است یا جای پارک نزدیک تری هم به سینما وجود دارد؛ بنابراین این شرط نمی تواند یک شرط توقف باشد.

wiki: زمان توقف
