زاویه های اویلر سه زاویه ای هستند که توسط لئونارد اویلر برای توصیف جهت گیری یک جسم صلب نسبت به یک سیستم مختصات ثابت معرفی شده اند. [ ۱] این زاویه ها در فیزیک می توانند نمایانگر جهت گیری یک چارچوب مرجع متحرک باشند یا در جبر خطی 3 بعدی این زاویه ها جهت گیری یک پایه را نشان می دهند.
زاویه های اویلر را می توان با هندسه ابتدایی یا با ترکیب چرخش ها تعریف کرد. تعریف هندسی نشان می دهد که سه دوران ابتدایی تشکیل شده ( دوران حول محورهای یک سیستم مختصات ) همواره برای دستیابی به هر چارچوب هدفی کافی هستند.
سه دوران ابتدایی می توانند بیرونی ( حول محورهای XYZ سیستم مختصات اصلی، که ثابت فرض می شود ) ، یا درونی ( حول محورهای XYZ سیستم مختصات در حال دوران، که با جسم در حال حرکت همبستگی دارد، و پس از هر دوران ابتدایی، جهت گیری آن تغییر می کند ) .
زاویه های اویلر معمولاً با α ، β ، γ یا φ ، θ ، ψ نشان داده می شوند. نویسندگان مختلف ممکن است از مجموعه محورهای دوران متفاوتی برای تعریف زاویه های اویلر بهره بگیرند یا نام های مختلف برای همین زاویه ها استفاده کنند. بنابراین، در هر بحثی که از زوایای اویلر استفاده می شود ، همواره باید آنها را در ابتدا تعریف نمود.
چنانچه دو قرارداد مختلف برای تعریف محورهای دوران ( ذاتی یا بیرونی ) را در نظر نگرفته باشیم، دوازده دنباله از محورهای دوران وجود خواهد داشت که به دو گروه تقسیم می شوند:
• زاویه های مناسب اویلر ( z - x - z, x - y - x, y - z - y, z - y - z, x - z - x, y - x - y )
• زاویه های تایت - برایان ( x - y - z, y - z - x, z - x - y, x - z - y, z - y - x, y - x - z )
زاویه های تایت - برایان، زاویه های کاردان، زاویه های دریایی، جهت ، ارتفاع، بانک یا pitch, yaw , و roll نیز نامیده می شوند. بعضی اوقات، هر دو نوع دنباله "زاویه های اویلر" خوانده می شوند. در این حالت، توالی گروه اول زاویه های مناسب یا کلاسیک اویلر نامیده می شود.
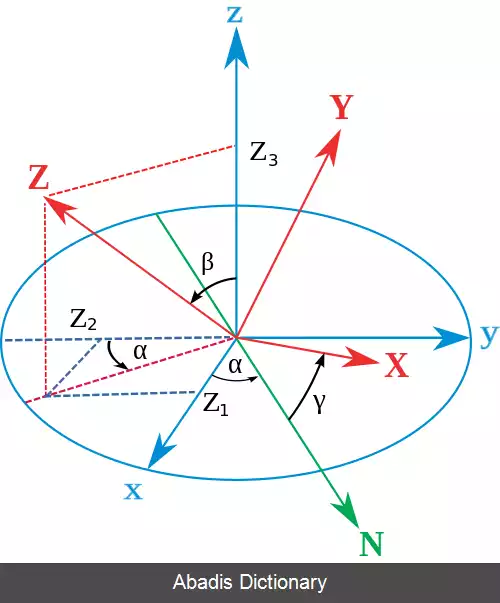
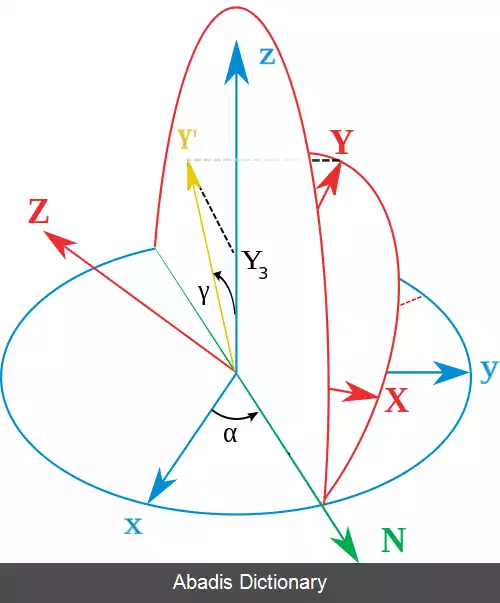
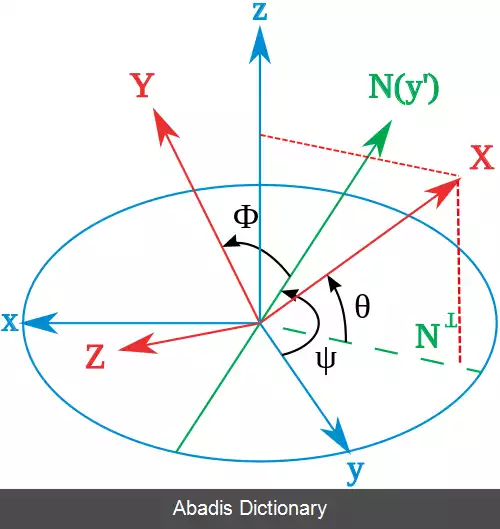
محورهای چارچوب اصلی با x ، y ، z و محورهای چارچوب چرخان با X ، Y ، Z نشان داده می شوند. تعریف هندسی ( که گاه به آن استاتیک گفته می شود ) با تعریف خط گره ها به عنوان فصل مشترک صفحات xy و XY آغاز می شود ( همچنین می توان آن را به عنوان عمود مشترک بر محورهای z و Z تعریف کرد و سپس به عنوان ضرب خارجی N = z × Z نوشت ) . با استفاده از این روش، سه زاویه اویلر را می توان به شرح زیر تعریف کرد: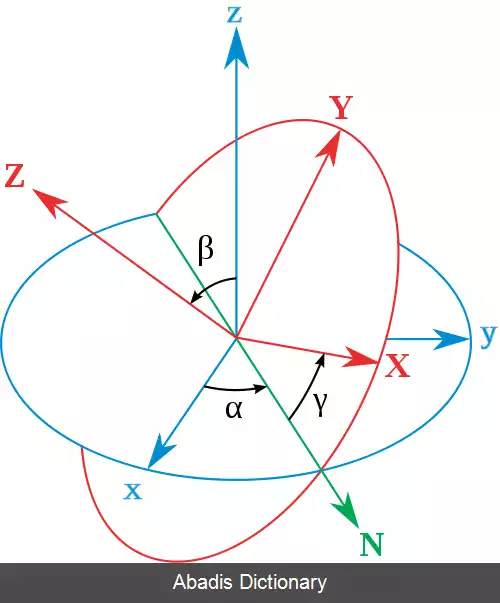
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفزاویه های اویلر را می توان با هندسه ابتدایی یا با ترکیب چرخش ها تعریف کرد. تعریف هندسی نشان می دهد که سه دوران ابتدایی تشکیل شده ( دوران حول محورهای یک سیستم مختصات ) همواره برای دستیابی به هر چارچوب هدفی کافی هستند.
سه دوران ابتدایی می توانند بیرونی ( حول محورهای XYZ سیستم مختصات اصلی، که ثابت فرض می شود ) ، یا درونی ( حول محورهای XYZ سیستم مختصات در حال دوران، که با جسم در حال حرکت همبستگی دارد، و پس از هر دوران ابتدایی، جهت گیری آن تغییر می کند ) .
زاویه های اویلر معمولاً با α ، β ، γ یا φ ، θ ، ψ نشان داده می شوند. نویسندگان مختلف ممکن است از مجموعه محورهای دوران متفاوتی برای تعریف زاویه های اویلر بهره بگیرند یا نام های مختلف برای همین زاویه ها استفاده کنند. بنابراین، در هر بحثی که از زوایای اویلر استفاده می شود ، همواره باید آنها را در ابتدا تعریف نمود.
چنانچه دو قرارداد مختلف برای تعریف محورهای دوران ( ذاتی یا بیرونی ) را در نظر نگرفته باشیم، دوازده دنباله از محورهای دوران وجود خواهد داشت که به دو گروه تقسیم می شوند:
• زاویه های مناسب اویلر ( z - x - z, x - y - x, y - z - y, z - y - z, x - z - x, y - x - y )
• زاویه های تایت - برایان ( x - y - z, y - z - x, z - x - y, x - z - y, z - y - x, y - x - z )
زاویه های تایت - برایان، زاویه های کاردان، زاویه های دریایی، جهت ، ارتفاع، بانک یا pitch, yaw , و roll نیز نامیده می شوند. بعضی اوقات، هر دو نوع دنباله "زاویه های اویلر" خوانده می شوند. در این حالت، توالی گروه اول زاویه های مناسب یا کلاسیک اویلر نامیده می شود.
محورهای چارچوب اصلی با x ، y ، z و محورهای چارچوب چرخان با X ، Y ، Z نشان داده می شوند. تعریف هندسی ( که گاه به آن استاتیک گفته می شود ) با تعریف خط گره ها به عنوان فصل مشترک صفحات xy و XY آغاز می شود ( همچنین می توان آن را به عنوان عمود مشترک بر محورهای z و Z تعریف کرد و سپس به عنوان ضرب خارجی N = z × Z نوشت ) . با استفاده از این روش، سه زاویه اویلر را می توان به شرح زیر تعریف کرد:




wiki: زاویه های اویلر
