زاویه محاطی
لغت نامه دهخدا
فرهنگ فارسی
دانشنامه عمومی
زاویهٔ محاطی در هندسه هنگامی ساخته می شود که دو خط گذرا از روی دایره ( یا در تباهیدگی یک خط قطع کننده و یک خط مماس ) با یکدیگر روی پیرامون دایره برخورد کنند.
به بیان ساده تر اگر یک زاویه درون یک دایره باشد و ضلع های زاویه، دو وتر از دایره باشد که با هم یک نقطهٔ مشترک دارند، چنین زاویه ای زاویهٔ محاطی نام دارد. در کتاب سوم اصول اقلیدس، گزاره های ۲۰ تا ۲۲، ویژگی های این زاویه گفته شده است. اگر یک زاویهٔ مرکزی و یک زاویهٔ محاطی هر دو یک کمان از دایره را دربرداشته باشند، اندازهٔ زاویهٔ محاطی نصف زاویهٔ مرکزی خواهد بود.
اگر O مرکز دایره باشد، دو نقطهٔ بر روی محیط دایره انتخاب کنید و آن ها را به ترتیب V و A بنامید. V را به O وصل کنید و آن را ادامه دهید تا با پیرامون دایره در نقطهٔ B برخورد کند. چون این خط از مرکز دایره گذشته است پس قطر دایره است در نتیجه V در یک سوی قطر و B در سوی دیگر آن جای گرفته است. حال زاویه ای بکشید که راس آن در نقطهٔ V باشد و دو لبهٔ آن از A و B بگذرد.
نقطهٔ A را به O وصل کنید. زاویهٔ BOA یک زاویهٔ مرکزی است. آن را θ بنامید. دو پاره خط OA و OV با هم برابرند چون هر دو شعاع دایره اند. پس مثلث VOA متساوی الساقین است. در نتیجه دو زاویهٔ BVA ( زاویهٔ محاطی ) و VAO با هم برابرند. هر دوی این زاویه ها را ψ می نامیم.
زاویه های BOA و AOV با هم مکمل اند و مجموع آن ها ۱۸۰ درجه می شود. چون خط VB از O می گذرد و یک خط راست است پس اندازهٔ زاویهٔ AOV از رابطهٔ ۱۸۰° − θ بدست می آید.
از سوی دیگر می دانیم که مجموع زاویه های داخلی مثلث ۱۸۰ درجه است. سه زاویهٔ داخلی مثلث VOA عبارتند از: ۱۸۰° − θ و ψ ، ψ. بنابراین:
۱۸۰° را از دو سوی تساوی کم می کنیم.
که در آن θ زاویهٔ مرکزی کمان AB است و ψ زاویهٔ محاطی همان کمان است که اندازه ای برابر با نصف آن دارد.
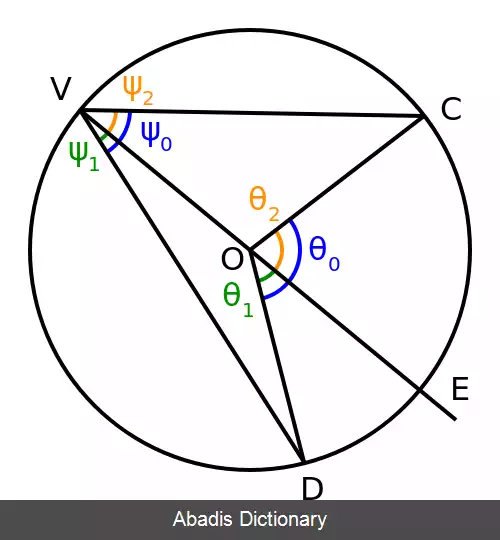
دایره ای با مرکز O را در نظر بگیرید. سه نقطهٔ V, C و D را بر روی آن برگزینید. دو پاره خط VC و VD را بکشید. زاویهٔ DVC یک زاویهٔ محاطی است. حال خط VO را بکشید و آن را ادامه دهید تا با سوی دیگر دایره در نقطهٔ E برخورد کند. کمان روبرو به زاویهٔ محاطی DVC، کمان DC نام دارد.
کمان DC نقطهٔ E را در بر می گیرد و می دانیم که این نقطه بر روی قطری از دایره قرار دارد. از سوی دیگر زاویه های DVE و EVC هر دو زاویهٔ محاطی اند. در بخش پیشین بدست آوردیم که اگر یک ضلع زاویهٔ محاطی از مرکز دایره بگذرد اندازهٔ آن برابر نصف کمان روبروی آن است. حال از داده های بخش پیشین بهره می گیریم: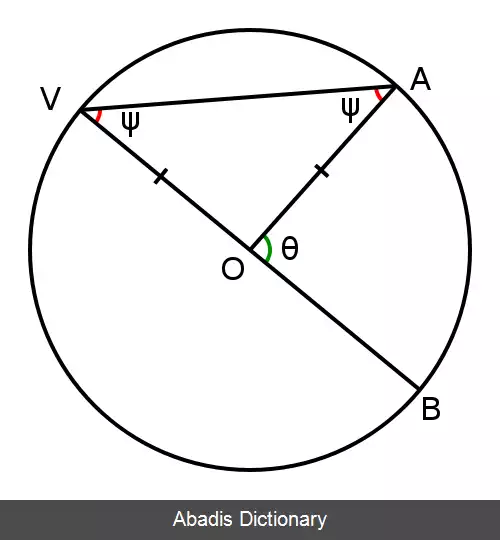

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه بیان ساده تر اگر یک زاویه درون یک دایره باشد و ضلع های زاویه، دو وتر از دایره باشد که با هم یک نقطهٔ مشترک دارند، چنین زاویه ای زاویهٔ محاطی نام دارد. در کتاب سوم اصول اقلیدس، گزاره های ۲۰ تا ۲۲، ویژگی های این زاویه گفته شده است. اگر یک زاویهٔ مرکزی و یک زاویهٔ محاطی هر دو یک کمان از دایره را دربرداشته باشند، اندازهٔ زاویهٔ محاطی نصف زاویهٔ مرکزی خواهد بود.
اگر O مرکز دایره باشد، دو نقطهٔ بر روی محیط دایره انتخاب کنید و آن ها را به ترتیب V و A بنامید. V را به O وصل کنید و آن را ادامه دهید تا با پیرامون دایره در نقطهٔ B برخورد کند. چون این خط از مرکز دایره گذشته است پس قطر دایره است در نتیجه V در یک سوی قطر و B در سوی دیگر آن جای گرفته است. حال زاویه ای بکشید که راس آن در نقطهٔ V باشد و دو لبهٔ آن از A و B بگذرد.
نقطهٔ A را به O وصل کنید. زاویهٔ BOA یک زاویهٔ مرکزی است. آن را θ بنامید. دو پاره خط OA و OV با هم برابرند چون هر دو شعاع دایره اند. پس مثلث VOA متساوی الساقین است. در نتیجه دو زاویهٔ BVA ( زاویهٔ محاطی ) و VAO با هم برابرند. هر دوی این زاویه ها را ψ می نامیم.
زاویه های BOA و AOV با هم مکمل اند و مجموع آن ها ۱۸۰ درجه می شود. چون خط VB از O می گذرد و یک خط راست است پس اندازهٔ زاویهٔ AOV از رابطهٔ ۱۸۰° − θ بدست می آید.
از سوی دیگر می دانیم که مجموع زاویه های داخلی مثلث ۱۸۰ درجه است. سه زاویهٔ داخلی مثلث VOA عبارتند از: ۱۸۰° − θ و ψ ، ψ. بنابراین:
۱۸۰° را از دو سوی تساوی کم می کنیم.
که در آن θ زاویهٔ مرکزی کمان AB است و ψ زاویهٔ محاطی همان کمان است که اندازه ای برابر با نصف آن دارد.
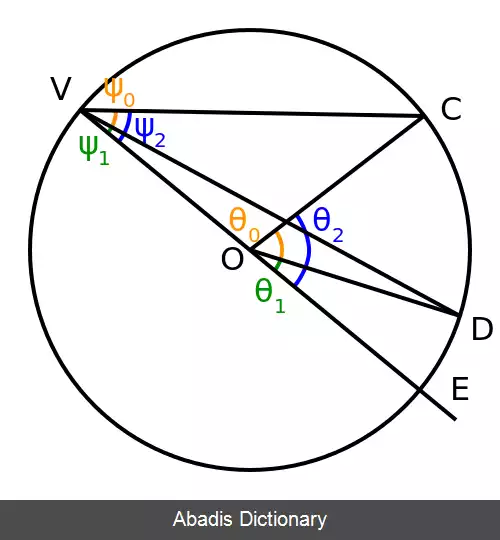
دایره ای با مرکز O را در نظر بگیرید. سه نقطهٔ V, C و D را بر روی آن برگزینید. دو پاره خط VC و VD را بکشید. زاویهٔ DVC یک زاویهٔ محاطی است. حال خط VO را بکشید و آن را ادامه دهید تا با سوی دیگر دایره در نقطهٔ E برخورد کند. کمان روبرو به زاویهٔ محاطی DVC، کمان DC نام دارد.
کمان DC نقطهٔ E را در بر می گیرد و می دانیم که این نقطه بر روی قطری از دایره قرار دارد. از سوی دیگر زاویه های DVE و EVC هر دو زاویهٔ محاطی اند. در بخش پیشین بدست آوردیم که اگر یک ضلع زاویهٔ محاطی از مرکز دایره بگذرد اندازهٔ آن برابر نصف کمان روبروی آن است. حال از داده های بخش پیشین بهره می گیریم:




wiki: زاویه محاطی
پیشنهاد کاربران
درون کنج، کنج درونی، گوشه درونی
