در علوم اخترشناسی ، ریشهٔ دوم یا جذر یا رادیکال ( به انگلیسی: Square root ) یک عدد حقیقی غیرمنفی x به صورت x نشان داده می شود و نتیجهٔ آن عددی حقیقی غیر منفی است که مجذورش ( عدد حاصل از ضرب یک عدد در خودش ) [ ۱] برابر x است.
برای مثال، جذر عدد ۹ برابر ۳ است ( به صورت 9 = 3 نمایش می یابد ) زیرا داریم: 3 2 = 3 × 3 = 9.
جذر اغلب در هنگام حل معادله درجه دوم یا معادله های به شکل a x 2 + b x + c = 0 استفاده می شود، زیرا متغیر x به توان دو رسیده است.
طبق قانون بنیادی جبری، دو جواب برای ریشهٔ دوم یک عدد وجود دارد ( این دو جواب در ریشهٔ دوم عدد صفر با هم یکی هستند ) . برای هر عدد حقیقی مثبت دو جواب برای ریشهٔ دوم وجود دارد که این دو جواب عددی هستند که یک بار منفی و یک بار مثبت است ( به شکل ± x ) .
ریشهٔ دوم اعدادی که مربع کامل نیستند همواره عددی گنگ است، یعنی اعداد را نمی توان به صورت کسری از دو عدد صحیح گویا کرد. برای مثال، 2 را نمی توان دقیقاً به صورت m n نوشت، که در آن n و m اعدادی صحیح هستند. در هر حال این عدد اندازه قطر مربعی به ضلع یک است. از مدت های گذشته، عدد 2 را عددی گنگ می دانستند و آن را به فیثاغورث نسبت می دادند.
نماد ریشهٔ دوم ( ) برای اولین بار در قرن شانزدهم استفاده شد. به نظر می رسد که این علامت از حرف کوچک r برگرفته شده است، که بیانگر واژه لاتین radix به معنای ریشه است.
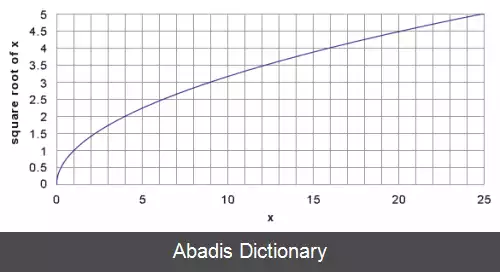
• تابع ریشه دوم، f ( x ) = x {\displaystyle f ( x ) ={\sqrt {x}}} ، تابعی است از مجموعه اعداد حقیقی غیرمنفی R + ∪ { 0 } {\displaystyle \mathbb {R} ^{+}\cup \{0\}} به خودش.
• تابع ریشه دوم f ( x ) = x {\displaystyle f ( x ) ={\sqrt {x}}} همواره مقداری منحصربه فرد برمی گرداند.
• برای به دست آوردن هر دو جواب ریشه دوم، ابتدا اولین جواب را به دست آورید و آن را x1 بنامید، سپس آن را از صفر کم کنید تا x2 به دست آید ( x2 = ۰ − x1 ) .
• خواص زیر، مهم ترین خواص ریشه دوم هستند که برای هر عدد حقیقی مثبت x {\displaystyle x} و y {\displaystyle y} صحیح هستند:
• ریشه دوم تابعی است از اعداد گویا به اعداد جبری. x {\displaystyle {\sqrt {x}}} عددی گویا است، اگر و تنها اگر x {\displaystyle x} عددی گویا باشد که بتوان آن را به صورت کسری از دو عدد مربع کامل نشان داد. به طور کلی، 2 {\displaystyle {\sqrt {2}}} عددی گنگ است.
• در هندسه، تابع ریشه دوم نگاشتی از سطح یک مربع به طول اضلاعش.
• خلاف یک اشتباه رایج، x 2 {\displaystyle {\sqrt {x^{2}}}} لزوماً برابر x {\displaystyle x} نیست. این برابری تنها در مواردی که x {\displaystyle x} غیرمنفی باشد صدق می کند. اما اگر x < 0 {\displaystyle x< 0} باشد، طبق تعریف x 2 {\displaystyle {\sqrt {x^{2}}}} است و این یعنی x 2 = − x {\displaystyle {\sqrt {x^{2}}}= - x} . در نتیجه برای هر عدد حقیقی x {\displaystyle x} داریم x 2 = | x | {\displaystyle {\sqrt {x^{2}}}=\left|x\right|} . ( قدرمطلق را ببینید )
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای مثال، جذر عدد ۹ برابر ۳ است ( به صورت 9 = 3 نمایش می یابد ) زیرا داریم: 3 2 = 3 × 3 = 9.
جذر اغلب در هنگام حل معادله درجه دوم یا معادله های به شکل a x 2 + b x + c = 0 استفاده می شود، زیرا متغیر x به توان دو رسیده است.
طبق قانون بنیادی جبری، دو جواب برای ریشهٔ دوم یک عدد وجود دارد ( این دو جواب در ریشهٔ دوم عدد صفر با هم یکی هستند ) . برای هر عدد حقیقی مثبت دو جواب برای ریشهٔ دوم وجود دارد که این دو جواب عددی هستند که یک بار منفی و یک بار مثبت است ( به شکل ± x ) .
ریشهٔ دوم اعدادی که مربع کامل نیستند همواره عددی گنگ است، یعنی اعداد را نمی توان به صورت کسری از دو عدد صحیح گویا کرد. برای مثال، 2 را نمی توان دقیقاً به صورت m n نوشت، که در آن n و m اعدادی صحیح هستند. در هر حال این عدد اندازه قطر مربعی به ضلع یک است. از مدت های گذشته، عدد 2 را عددی گنگ می دانستند و آن را به فیثاغورث نسبت می دادند.
نماد ریشهٔ دوم ( ) برای اولین بار در قرن شانزدهم استفاده شد. به نظر می رسد که این علامت از حرف کوچک r برگرفته شده است، که بیانگر واژه لاتین radix به معنای ریشه است.
• تابع ریشه دوم، f ( x ) = x {\displaystyle f ( x ) ={\sqrt {x}}} ، تابعی است از مجموعه اعداد حقیقی غیرمنفی R + ∪ { 0 } {\displaystyle \mathbb {R} ^{+}\cup \{0\}} به خودش.
• تابع ریشه دوم f ( x ) = x {\displaystyle f ( x ) ={\sqrt {x}}} همواره مقداری منحصربه فرد برمی گرداند.
• برای به دست آوردن هر دو جواب ریشه دوم، ابتدا اولین جواب را به دست آورید و آن را x1 بنامید، سپس آن را از صفر کم کنید تا x2 به دست آید ( x2 = ۰ − x1 ) .
• خواص زیر، مهم ترین خواص ریشه دوم هستند که برای هر عدد حقیقی مثبت x {\displaystyle x} و y {\displaystyle y} صحیح هستند:
• ریشه دوم تابعی است از اعداد گویا به اعداد جبری. x {\displaystyle {\sqrt {x}}} عددی گویا است، اگر و تنها اگر x {\displaystyle x} عددی گویا باشد که بتوان آن را به صورت کسری از دو عدد مربع کامل نشان داد. به طور کلی، 2 {\displaystyle {\sqrt {2}}} عددی گنگ است.
• در هندسه، تابع ریشه دوم نگاشتی از سطح یک مربع به طول اضلاعش.
• خلاف یک اشتباه رایج، x 2 {\displaystyle {\sqrt {x^{2}}}} لزوماً برابر x {\displaystyle x} نیست. این برابری تنها در مواردی که x {\displaystyle x} غیرمنفی باشد صدق می کند. اما اگر x < 0 {\displaystyle x< 0} باشد، طبق تعریف x 2 {\displaystyle {\sqrt {x^{2}}}} است و این یعنی x 2 = − x {\displaystyle {\sqrt {x^{2}}}= - x} . در نتیجه برای هر عدد حقیقی x {\displaystyle x} داریم x 2 = | x | {\displaystyle {\sqrt {x^{2}}}=\left|x\right|} . ( قدرمطلق را ببینید )


wiki: ریشه دوم
