رگرسیون خط الرأس. رگرسیون خط الرأس روشی برای تخمین ضرایب مدل های رگرسیون چندگانه در حالتی است که متغیرهای مستقل، همبستگی بالایی دارند. در اینجا روش کار مشابه کمترین مربعات است اما برخی ضرایب تخمین زده شده را با هم به سمت صفر سوق می دهیم. این روش در بسیاری از زمینه ها از جمله اقتصاد سنجی، شیمی و مهندسی مورد استفاده قرار می گیرد. نام دیگر آن نرمال سازی تیخونوف، که به نام آندری تیخونف نامگذاری شده، است و روشی برای نرمال سازی مسائل غیر خوش ساخت می باشد و به ویژه برای کاهش مشکل هم خطی چندگانه در رگرسیون خطی مفید است، که معمولاً در مدل هایی با تعداد زیادی پارامتر رخ می دهد. به طور کلی، این روش کارایی بهتری را در مسائل تخمین پارامتر در ازای مقدار قابل قبولی اریبی ارائه می دهد ( به مبادله بایاس - واریانس مراجعه کنید ) .
این نظریه برای اولین بار توسط هورل و کنارد در سال ۱۹۷۰ در مقالات تکنومتریکس: "رگرسیون خط الرأس: تخمین اریب مسائل نامتعامد" و "رگرسیون خط الرأس: کاربردها در مسائل نامتعامد" معرفی شد. [ ۱] [ ۲]
رگرسیون خط الرأس به عنوان یک راه حل برای نادقیق بودن برآوردگرهای حداقل مربعات زمانی که مدل های رگرسیون خطی دارای متغیرهای مستقل هم خطی ( بسیار همبسته ) هستند ارائه شد. این امر تخمین دقیق تری از پارامترهای خط الراس ارائه می دهد، زیرا واریانس و برآوردگر میانگین مربعات آن اغلب کوچکتر از برآوردگرهای حداقل مربعی است که قبلاً مشتق شده بود.
در ساده ترین حالت، مسئله یک ماتریس لحظه ای وارون پذیر ( X T X ) با افزودن عناصر مثبت به قطر اصلی و در نتیجه شماره وضعیت آن کاهش می یابد. مشابه برآوردگر کمترین مربعات معمولی ، تخمین گر خط الرأس ساده به صورت ذیل می باشد
β ^ R = ( X T X + λ I ) − 1 X T y
که y پسرفت، X ماتریس طرح ، I ماتریس همانی و لامبدا پارامتر خط الرأس ، λ ≥ 0 به عنوان ثابت جابجایی قطرهای ماتریس همانی عمل می کند. [ ۳] می توان نشان داد که این تخمینگر راه حلی برای مسئله کمترین مربعات مقید به β T β = c که می توان آن را به صورت لاگرانژین بیان کرد:
min β ( y − X β ) T ( y − X β ) + λ ( β T β − c )
که نشان می دهد λ چیزی جز ضریب لاگرانژی از قید نیست. [ ۴] به طور معمول، λ بر اساس یک معیار اکتشافی یا هیوریستیک انتخاب می شود، که در این صورت قید به طور کامل ارضا نمی شود. به طور خاص در مورد λ = 0 ، که در آن قید غیر الزام آور است ، تخمینگر خط الرأس به کمترین مربعات معمولی کاهش می یابد. یک رویکرد کلی تر از تنظیم تیخونوف در زیر مورد بحث قرار می گیرد.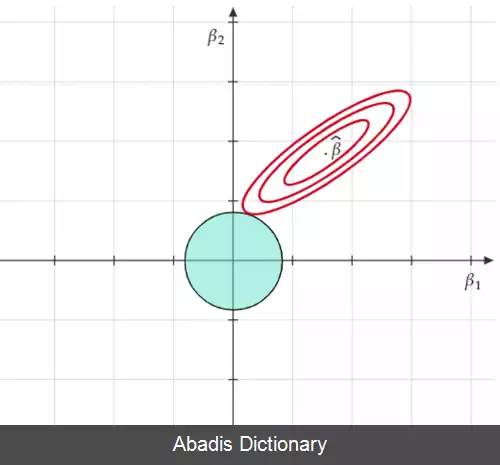
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین نظریه برای اولین بار توسط هورل و کنارد در سال ۱۹۷۰ در مقالات تکنومتریکس: "رگرسیون خط الرأس: تخمین اریب مسائل نامتعامد" و "رگرسیون خط الرأس: کاربردها در مسائل نامتعامد" معرفی شد. [ ۱] [ ۲]
رگرسیون خط الرأس به عنوان یک راه حل برای نادقیق بودن برآوردگرهای حداقل مربعات زمانی که مدل های رگرسیون خطی دارای متغیرهای مستقل هم خطی ( بسیار همبسته ) هستند ارائه شد. این امر تخمین دقیق تری از پارامترهای خط الراس ارائه می دهد، زیرا واریانس و برآوردگر میانگین مربعات آن اغلب کوچکتر از برآوردگرهای حداقل مربعی است که قبلاً مشتق شده بود.
در ساده ترین حالت، مسئله یک ماتریس لحظه ای وارون پذیر ( X T X ) با افزودن عناصر مثبت به قطر اصلی و در نتیجه شماره وضعیت آن کاهش می یابد. مشابه برآوردگر کمترین مربعات معمولی ، تخمین گر خط الرأس ساده به صورت ذیل می باشد
β ^ R = ( X T X + λ I ) − 1 X T y
که y پسرفت، X ماتریس طرح ، I ماتریس همانی و لامبدا پارامتر خط الرأس ، λ ≥ 0 به عنوان ثابت جابجایی قطرهای ماتریس همانی عمل می کند. [ ۳] می توان نشان داد که این تخمینگر راه حلی برای مسئله کمترین مربعات مقید به β T β = c که می توان آن را به صورت لاگرانژین بیان کرد:
min β ( y − X β ) T ( y − X β ) + λ ( β T β − c )
که نشان می دهد λ چیزی جز ضریب لاگرانژی از قید نیست. [ ۴] به طور معمول، λ بر اساس یک معیار اکتشافی یا هیوریستیک انتخاب می شود، که در این صورت قید به طور کامل ارضا نمی شود. به طور خاص در مورد λ = 0 ، که در آن قید غیر الزام آور است ، تخمینگر خط الرأس به کمترین مربعات معمولی کاهش می یابد. یک رویکرد کلی تر از تنظیم تیخونوف در زیر مورد بحث قرار می گیرد.

wiki: رگرسیون خط الرأس
