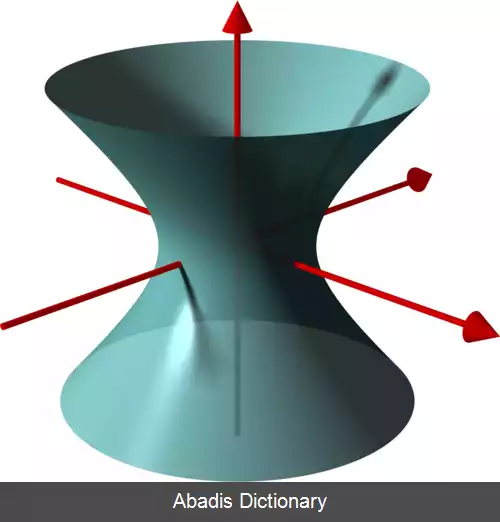
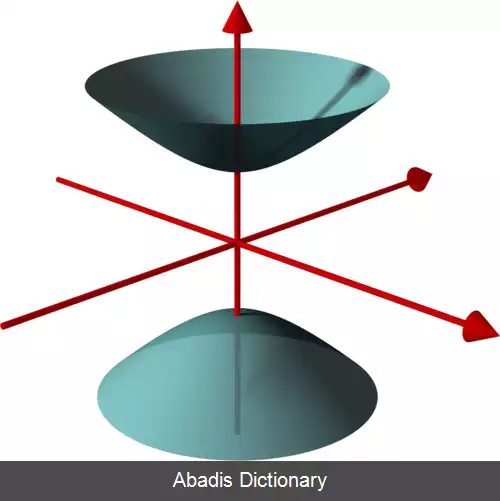
در فضای اقلیدسی رویه دورانی ( به انگلیسی: Surface of Revolution ) ( یا سطح دَوَرانی ) ، رویه ای است که حاصل چرخاندن یک منحنی ( موسوم به منحنی مولد ) حول یک محور ثابت است. رویه های دورانی همواره تقارن چرخشی دارند.
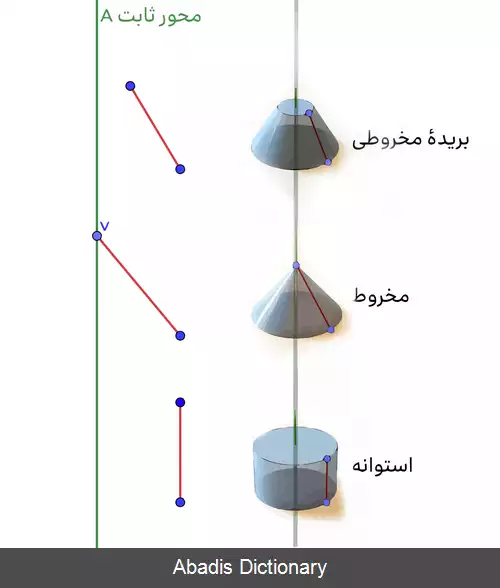
رویه های دورانی را می توان با چرخاندن منحنی مولد c به دور محور ثابت A ساخت. هر نقطهٔ p از منحنی c معرف دایرهٔ C p است که در صفحهٔ S عمود بر محور A قرار می گیرد. ازاین رو هر رویه دورانی شامل مجموعه ای است از دایره ها در صفحات موازی، که «دایره های موازی» نام دارند. [ ۱]
صفحات M ، که محور A را بر روی خود دارند، رویه S را در منحنی های همنهشت m ( موسوم به «منحنی های نصف النهاری» ) [ الف] قطع می کنند. صفحه های S ( شامل دایرهٔ C p ) و صفحه های M ( شامل منحنی های نصف النهاری m ) برهم عمودند. ازاین رو هر منحنی نصف النهاری و دایرهٔ موازی با یکدیگر تشکیل زاویه قائمه می دهند. از مجموعهٔ منحنی های نصف النهاری و دایره های موازی روی رویه شبکه ای از منحنی های عمودبرهم تشکیل می شود. [ ۲]
صفحهٔ T p مماس بر نقطهٔ p یک رویه دورانی را می توان با خط t c مماس بر دایرهٔ C p و خط t m مماس بر منحنی نیم روزی m تعریف کرد. در هر نقطهٔ p ، خط قائم n p بر خط مماس t c عمود است، بنابراین n p روی صفحهٔ نصف النهاری M است و محور A را در نقطهٔ مرکز کره ای قطع می کند که p روی رویه آن است. این کره و رویه دورانی در یکی از دایره های موازی مماسند. [ ۳]
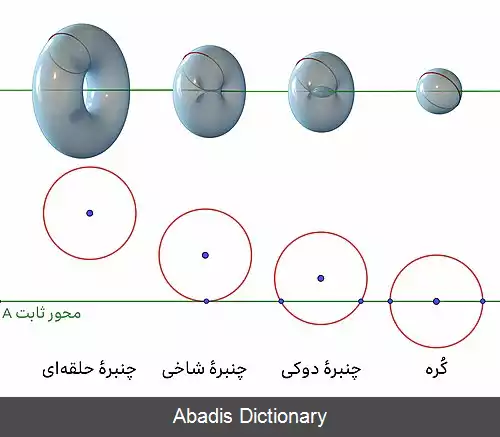
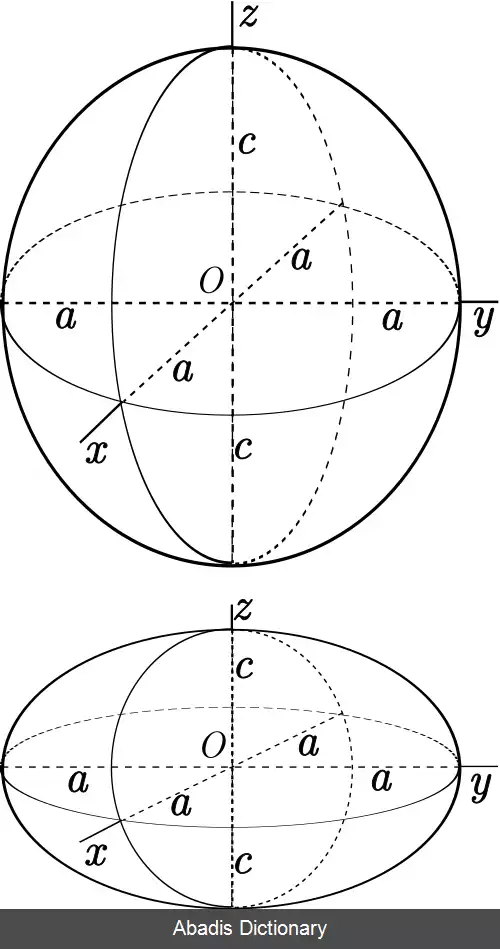
از آنجا که منحنی های نصف النهاری بهتر از دیگر منحنی ها نشانگر شکل نهایی سطحند، بهتر است در ایجاد رویه های دورانی از این منحنی ها استفاده شود. منحنی های نصف النهاری نسبت به محور دوران متقارنند، هر کدام از بخش های تقارن «منحنی نیم نصف النهاری»[ ب] نام دارد. برای ایجاد رویه دورانی منحنی نصف النهاری را باید ۳۶۰° و منحنی های نیم نصف النهاری را ۱۸۰° درجه چرخاند. [ ۴]
اگر منحنی های نصف النهاری و محور دوران همدیگر را با زاویه ای به غیر از زاویهٔ ۹۰° همدیگر را قطع کنند، یک نقطه منفرد روی دورانی تشکیل می شود. [ ۵]
اگر r = x 2 + y 2 فاصله نقطه ای روی رویه از محور ثابت باشد، معادلهٔ صریح رویه دورانی به شکل زیر نوشته می شود:[ ۶]
برای یافتن معادله پارامتری یک رویه دورانی، باید ماتریس دوران حول محور را بر منحنی مولد c اعمال کرد. فرض می شود محور ثابت محور - های مختصاتی باشد. معادلهٔ دوران حول محور - ها عبارت است از: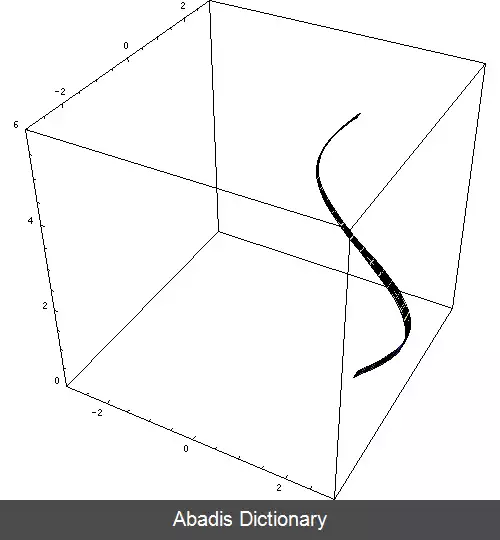
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفرویه های دورانی را می توان با چرخاندن منحنی مولد c به دور محور ثابت A ساخت. هر نقطهٔ p از منحنی c معرف دایرهٔ C p است که در صفحهٔ S عمود بر محور A قرار می گیرد. ازاین رو هر رویه دورانی شامل مجموعه ای است از دایره ها در صفحات موازی، که «دایره های موازی» نام دارند. [ ۱]
صفحات M ، که محور A را بر روی خود دارند، رویه S را در منحنی های همنهشت m ( موسوم به «منحنی های نصف النهاری» ) [ الف] قطع می کنند. صفحه های S ( شامل دایرهٔ C p ) و صفحه های M ( شامل منحنی های نصف النهاری m ) برهم عمودند. ازاین رو هر منحنی نصف النهاری و دایرهٔ موازی با یکدیگر تشکیل زاویه قائمه می دهند. از مجموعهٔ منحنی های نصف النهاری و دایره های موازی روی رویه شبکه ای از منحنی های عمودبرهم تشکیل می شود. [ ۲]
صفحهٔ T p مماس بر نقطهٔ p یک رویه دورانی را می توان با خط t c مماس بر دایرهٔ C p و خط t m مماس بر منحنی نیم روزی m تعریف کرد. در هر نقطهٔ p ، خط قائم n p بر خط مماس t c عمود است، بنابراین n p روی صفحهٔ نصف النهاری M است و محور A را در نقطهٔ مرکز کره ای قطع می کند که p روی رویه آن است. این کره و رویه دورانی در یکی از دایره های موازی مماسند. [ ۳]
از آنجا که منحنی های نصف النهاری بهتر از دیگر منحنی ها نشانگر شکل نهایی سطحند، بهتر است در ایجاد رویه های دورانی از این منحنی ها استفاده شود. منحنی های نصف النهاری نسبت به محور دوران متقارنند، هر کدام از بخش های تقارن «منحنی نیم نصف النهاری»[ ب] نام دارد. برای ایجاد رویه دورانی منحنی نصف النهاری را باید ۳۶۰° و منحنی های نیم نصف النهاری را ۱۸۰° درجه چرخاند. [ ۴]
اگر منحنی های نصف النهاری و محور دوران همدیگر را با زاویه ای به غیر از زاویهٔ ۹۰° همدیگر را قطع کنند، یک نقطه منفرد روی دورانی تشکیل می شود. [ ۵]
اگر r = x 2 + y 2 فاصله نقطه ای روی رویه از محور ثابت باشد، معادلهٔ صریح رویه دورانی به شکل زیر نوشته می شود:[ ۶]
برای یافتن معادله پارامتری یک رویه دورانی، باید ماتریس دوران حول محور را بر منحنی مولد c اعمال کرد. فرض می شود محور ثابت محور - های مختصاتی باشد. معادلهٔ دوران حول محور - ها عبارت است از:






wiki: رویه دورانی
