در آنالیز عددی روش نیوتن ، که همچنین به عنوان روش نیوتن - رافسون ( به انگلیسی: Newton - Raphson method ) نیز شناخته میشود الگوریتم ریشه یابی است که تقریب های خوبی در نزدیکی ریشه یک تابع ( صفرهای یک تابع ) میزند. در پایه ای ترین حالت، الگوریتم نیوتن برای یک تابعی چون f با متغیر x و با مشتق f ′ به همراه حدس اولیه x 0 بکار میرود. اگر تابع حدس کافی و دقیقی را برآورد سازد و همچنین حدس اولیه نزدیک به ریشه تابع مفروض باشد ( که با همگرایی تقریب ها این موضوع روشن می شود ) آنگاه x 1 تقریب بهتری نسبت به x 0 به حساب می آید. چرا که با احتساب همگرایی جواب ها، هر تقریب نسبت به تقریب قبل از خودش از دقت بالاتری برخوردار بوده و به ریشه تابع نزدیک تر است. به لحاظ هندسی ( x 1 , 0 ) نقطه ای است که محور x و خط مماس تابع f در نقطهٔ ( x 0 , f ( x 0 ) ) یکدیگر را قطع میکنند. شکل عمومی الگوریتم نیوتن به شرح زیر میباشد:
که در اصل از رابطه f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 1 ! بدست امده است. میدانیم که در نقطهٔ برخورد تابع با محور x مقدار تابع صفر خواهد بود لذا 0 = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 1 ! که در آخر با تقسیم بر f ′ ( x 0 ) میتوان رابطه را به فرم رو به رو بازنویسی کرد:
همانطور که مشهود است روش نیوتن - رافسون از سری تیلور ناقص تابع مفروض به عنوان یک تقریب خطی حول نقطهٔ حدس اولیه x 0 بهره میبرد و از این جهت تقریب را ناقص میگویند که نیازی به نوشتن سری تابع تا مراتب بالاتر نبوده و به همان دو جمله ابتدایی بسنده میکند که این موضوع نیز دلیلی بر تقریب خطی بودن روش نیوتن میباشد. همچنین چون این روش معادلهٔ یک تابع را تا معادلهٔ یک تابع درجه یک تقیل میدهد، لذا صرف نظر از اینکه تابع چند ریشه دارد، در نهایت الگوریتم تنها یک جواب بدست می آورد.
این روش همچنین میتواند در توابع مختلط و دستگاه معادلات بکار رود.
ساز و کار روش نیوتن شروع مراحل تخمین ریشه با انتخاب یک حدس اولیه است که به اندازه لازم به مقدار واقعی ریشه نزدیک باشد ، سپس میتوان با استفاده از خط مماس تابع را تقریب زد و نهایتاً با توجه به خط مماس طول از مبدا ( ریشه تقریب خطی ) را معین ساخت. ریشه تقریب معمولاً تقریب بهتری از ریشه واقعی تابع نسبت به حدس اولیه است و الگوریتم به همین منوال میتواند تکرار شود.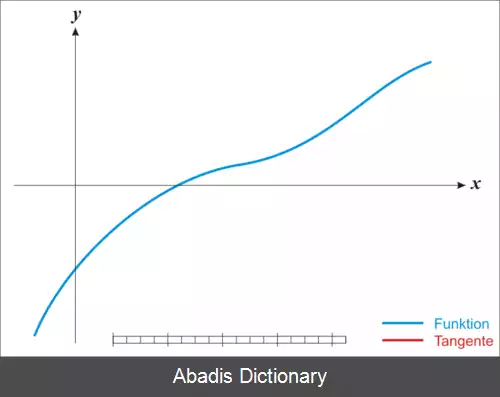
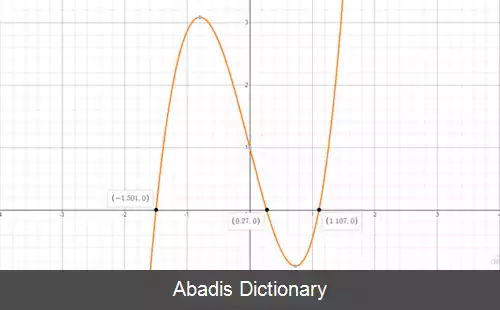
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکه در اصل از رابطه f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 1 ! بدست امده است. میدانیم که در نقطهٔ برخورد تابع با محور x مقدار تابع صفر خواهد بود لذا 0 = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 1 ! که در آخر با تقسیم بر f ′ ( x 0 ) میتوان رابطه را به فرم رو به رو بازنویسی کرد:
همانطور که مشهود است روش نیوتن - رافسون از سری تیلور ناقص تابع مفروض به عنوان یک تقریب خطی حول نقطهٔ حدس اولیه x 0 بهره میبرد و از این جهت تقریب را ناقص میگویند که نیازی به نوشتن سری تابع تا مراتب بالاتر نبوده و به همان دو جمله ابتدایی بسنده میکند که این موضوع نیز دلیلی بر تقریب خطی بودن روش نیوتن میباشد. همچنین چون این روش معادلهٔ یک تابع را تا معادلهٔ یک تابع درجه یک تقیل میدهد، لذا صرف نظر از اینکه تابع چند ریشه دارد، در نهایت الگوریتم تنها یک جواب بدست می آورد.
این روش همچنین میتواند در توابع مختلط و دستگاه معادلات بکار رود.
ساز و کار روش نیوتن شروع مراحل تخمین ریشه با انتخاب یک حدس اولیه است که به اندازه لازم به مقدار واقعی ریشه نزدیک باشد ، سپس میتوان با استفاده از خط مماس تابع را تقریب زد و نهایتاً با توجه به خط مماس طول از مبدا ( ریشه تقریب خطی ) را معین ساخت. ریشه تقریب معمولاً تقریب بهتری از ریشه واقعی تابع نسبت به حدس اولیه است و الگوریتم به همین منوال میتواند تکرار شود.


wiki: روش نیوتن
