در تجزیه و تحلیل عددی و آمار محاسباتی، روش نمونه برداری بازپس زننده یک تکنیک اساسی است که برای تولید مشاهدات از یک توزیع استفاده می شود.
در آنالیز عددی و محاسبات آماری، نمونه برداری بازپس زننده ( به انگلیسی: rejection sampling ) روش پایه ای برای تولید نمونه از یک توزیع احتمالی است که در آن به جای نمونه برداری مستقیم از توزیع P ( x ) که دشوار است، از توزیع پیشنهادی Q ( x ) که نمونه برداری از آن ساده است استفاده می شود. اما توزیع پیشنهادی Q ( x ) باید به گونه ای انتخاب شود که حداقل یک مقدار k وجود داشته باشد به طوریکه k Q ( x ) ≥ P ~ ( x ) . با استفاده از توزیع Q ( x ) نمونه x ∗ را بدست می آوریم اما این نمونه با احتمال P ~ ( x ∗ ) k Q ( x ∗ ) پذیرفته می شود. دلیل استفاده از P ~ ( x ) بجای P ( x ) این است که با توجه به رابطه P ( x ) = P ~ ( x ) Z نمونه برداری از P ~ ( x ) ساده تر از P ( x ) است. [ ۱]
در این روش احتمال تولید شدن یک نمونه دقبقا برابر با P ( x ) است.
P ~ ( x ) k Q ( x ) Q ( x ) ∫ P ~ ( x ) k Q ( x ) Q ( x ) d x = P ~ ( x ) ∫ P ~ ( x ) d x = P ( x )
همچنین احتمال پذیرش هر نمونه برابر است با:
P ( a c c e p t ) = ∫ P ~ ( x ) k Q ( x ) Q ( x ) d x = ∫ P ~ ( x ) d x k
به عبارت دیگر با افزایش مقدار k احتمال پذیرش نمونه ها کاهش می یابد. [ ۱]
چالش اصلی در روش نمونه برداری بازپس زننده تعیین توزیع پیشنهادی مناسب Q ( x ) است. بطوریکه مقدار k بگونه ای انتخاب شود که احتمال پذیرفته نشدن نمونه ها کاهش چشمگیری نداشته باشد. به عبارت دیگر k Q ( x ) در قسمت بالای منحنی P ( x ) قرار بگیرد و همچنین فاصله زیادی از آن نداشته باشد. در صورتیکه P ( x ) لگاریتم - مقعر باشد ( به انگلیسی: log - concave ) باشد با استفاده از روش نمونه برداری بازپس زننده تطبیقی ( به انگلیسی: Adaptive rejection sampling ) می توان توزیع پیشنهادی Q ( x ) مناسب را بدست آورد. [ ۱]
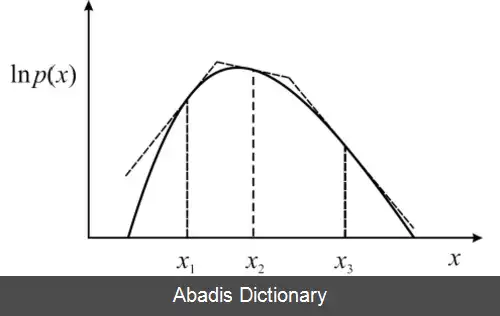
ابتدا با استفاده از توزیع یکنواخت تعدادی نمونه تولید می کنیم و برحسب احتمال گفته شده نمونه ها را پذیرش و یا رد می کنیم. در صورت پذیرفته نشدن هر نمونه یک خط مماس بر توزیع اصلی در آن نقطه رسم می کنیم. درنتیجه از تقاطع حاصل از این خطوط یک توزیع حاصل می شود. با نمونه برداری از این توزیع و پذیرفتن نمونه ها برحسب نسبت گفته شده، درصورت پذیرفته نشدن هر نمونه یک خط مماس جدید بر توزیع بدست آمده رسم می کنیم و فرآیند به همین ترتیب ادامه می یابد. با افزایش تعداد خطوط مماس، توزیع پیشنهادی بدست آمده پیچیده تر می شود. اما باید توجه داشت که این خطوط در مقیاس لگاریتم رسم می شوند. در واقع با اجرای این فرآیند توزیعی بدست خواهد آمد که در مقیاس معمولی تکه ای نمایی ( به انگلیسی: piecewise exponential ) است، که نمونه برداری از آن کار دشواری نیست. [ ۱]
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر آنالیز عددی و محاسبات آماری، نمونه برداری بازپس زننده ( به انگلیسی: rejection sampling ) روش پایه ای برای تولید نمونه از یک توزیع احتمالی است که در آن به جای نمونه برداری مستقیم از توزیع P ( x ) که دشوار است، از توزیع پیشنهادی Q ( x ) که نمونه برداری از آن ساده است استفاده می شود. اما توزیع پیشنهادی Q ( x ) باید به گونه ای انتخاب شود که حداقل یک مقدار k وجود داشته باشد به طوریکه k Q ( x ) ≥ P ~ ( x ) . با استفاده از توزیع Q ( x ) نمونه x ∗ را بدست می آوریم اما این نمونه با احتمال P ~ ( x ∗ ) k Q ( x ∗ ) پذیرفته می شود. دلیل استفاده از P ~ ( x ) بجای P ( x ) این است که با توجه به رابطه P ( x ) = P ~ ( x ) Z نمونه برداری از P ~ ( x ) ساده تر از P ( x ) است. [ ۱]
در این روش احتمال تولید شدن یک نمونه دقبقا برابر با P ( x ) است.
P ~ ( x ) k Q ( x ) Q ( x ) ∫ P ~ ( x ) k Q ( x ) Q ( x ) d x = P ~ ( x ) ∫ P ~ ( x ) d x = P ( x )
همچنین احتمال پذیرش هر نمونه برابر است با:
P ( a c c e p t ) = ∫ P ~ ( x ) k Q ( x ) Q ( x ) d x = ∫ P ~ ( x ) d x k
به عبارت دیگر با افزایش مقدار k احتمال پذیرش نمونه ها کاهش می یابد. [ ۱]
چالش اصلی در روش نمونه برداری بازپس زننده تعیین توزیع پیشنهادی مناسب Q ( x ) است. بطوریکه مقدار k بگونه ای انتخاب شود که احتمال پذیرفته نشدن نمونه ها کاهش چشمگیری نداشته باشد. به عبارت دیگر k Q ( x ) در قسمت بالای منحنی P ( x ) قرار بگیرد و همچنین فاصله زیادی از آن نداشته باشد. در صورتیکه P ( x ) لگاریتم - مقعر باشد ( به انگلیسی: log - concave ) باشد با استفاده از روش نمونه برداری بازپس زننده تطبیقی ( به انگلیسی: Adaptive rejection sampling ) می توان توزیع پیشنهادی Q ( x ) مناسب را بدست آورد. [ ۱]
ابتدا با استفاده از توزیع یکنواخت تعدادی نمونه تولید می کنیم و برحسب احتمال گفته شده نمونه ها را پذیرش و یا رد می کنیم. در صورت پذیرفته نشدن هر نمونه یک خط مماس بر توزیع اصلی در آن نقطه رسم می کنیم. درنتیجه از تقاطع حاصل از این خطوط یک توزیع حاصل می شود. با نمونه برداری از این توزیع و پذیرفتن نمونه ها برحسب نسبت گفته شده، درصورت پذیرفته نشدن هر نمونه یک خط مماس جدید بر توزیع بدست آمده رسم می کنیم و فرآیند به همین ترتیب ادامه می یابد. با افزایش تعداد خطوط مماس، توزیع پیشنهادی بدست آمده پیچیده تر می شود. اما باید توجه داشت که این خطوط در مقیاس لگاریتم رسم می شوند. در واقع با اجرای این فرآیند توزیعی بدست خواهد آمد که در مقیاس معمولی تکه ای نمایی ( به انگلیسی: piecewise exponential ) است، که نمونه برداری از آن کار دشواری نیست. [ ۱]


