درونیابی دومکعبی در ریاضیات توسعه ای بر درونیابی مکعبی است که بر روی نقاط جدول معمولی دو بعدی عمل می کند. سطح بدست آمده با استفاده از این درونیابی نرم تر از سطح بدست آمده توسط درونیابی های دیگر مانند درونیابی نزدیکترین همسایه یا درونیابی دو خطی است.
در کاربردهای پردازش تصویر در صورتی که نیاز به سرعت نباشد به طور معمول از این درونیابی استفاده خواهد. این درونیابی به جای ۴ نقطه درونیابی دوخطی از ۱۶ نقطه همجوار برای انجام درونیابی استفاده می کند.
فرض کنید مقادیر تابع f و مشتقات f x ، f y و f x y در چهار گوشه ( 0 , 0 ) ، ( 1 , 0 ) ، ( 0 , 1 ) و ( 1 , 1 ) مربع واحد مشخص باشد. در این صورت سطح درونیابی شده را می توان نوشت
درونیابی متشکل از مشخص کردن مقادیر ضرایب ناشناخته a i j است. تطبیق p ( x , y ) با مقادیر تابع معادلات زیر را به وجود خواهد آورد:
• f ( 0 , 0 ) = p ( 0 , 0 ) = a 00 {\displaystyle f ( 0, 0 ) =p ( 0, 0 ) =a_{00}}
• f ( 1 , 0 ) = p ( 1 , 0 ) = a 00 + a 10 + a 20 + a 30 {\displaystyle f ( 1, 0 ) =p ( 1, 0 ) =a_{00}+a_{10}+a_{20}+a_{30}}
• f ( 0 , 1 ) = p ( 0 , 1 ) = a 00 + a 01 + a 02 + a 03 {\displaystyle f ( 0, 1 ) =p ( 0, 1 ) =a_{00}+a_{01}+a_{02}+a_{03}}
• f ( 1 , 1 ) = p ( 1 , 1 ) = ∑ i = 0 3 ∑ j = 0 3 a i j {\displaystyle f ( 1, 1 ) =p ( 1, 1 ) =\textstyle \sum _{i=0}^{3}\sum _{j=0}^{3}a_{ij}}
به همین شکل مشتق ها در سمت x و سمت y بدست می آیند:
• f x ( 0 , 0 ) = p x ( 0 , 0 ) = a 10 {\displaystyle f_{x} ( 0, 0 ) =p_{x} ( 0, 0 ) =a_{10}}
• f x ( 1 , 0 ) = p x ( 1 , 0 ) = a 10 + 2 a 20 + 3 a 30 {\displaystyle f_{x} ( 1, 0 ) =p_{x} ( 1, 0 ) =a_{10}+2a_{20}+3a_{30}}
• f x ( 0 , 1 ) = p x ( 0 , 1 ) = a 10 + a 11 + a 12 + a 13 {\displaystyle f_{x} ( 0, 1 ) =p_{x} ( 0, 1 ) =a_{10}+a_{11}+a_{12}+a_{13}}
• f x ( 1 , 1 ) = p x ( 1 , 1 ) = ∑ i = 1 3 ∑ j = 0 3 a i j i {\displaystyle f_{x} ( 1, 1 ) =p_{x} ( 1, 1 ) =\textstyle \sum _{i=1}^{3}\sum _{j=0}^{3}a_{ij}i}
• f y ( 0 , 0 ) = p y ( 0 , 0 ) = a 01 {\displaystyle f_{y} ( 0, 0 ) =p_{y} ( 0, 0 ) =a_{01}}
• f y ( 1 , 0 ) = p y ( 1 , 0 ) = a 01 + a 11 + a 21 + a 31 {\displaystyle f_{y} ( 1, 0 ) =p_{y} ( 1, 0 ) =a_{01}+a_{11}+a_{21}+a_{31}}
• f y ( 0 , 1 ) = p y ( 0 , 1 ) = a 01 + 2 a 02 + 3 a 03 {\displaystyle f_{y} ( 0, 1 ) =p_{y} ( 0, 1 ) =a_{01}+2a_{02}+3a_{03}}
• f y ( 1 , 1 ) = p y ( 1 , 1 ) = ∑ i = 0 3 ∑ j = 1 3 a i j j {\displaystyle f_{y} ( 1, 1 ) =p_{y} ( 1, 1 ) =\textstyle \sum _{i=0}^{3}\sum _{j=1}^{3}a_{ij}j}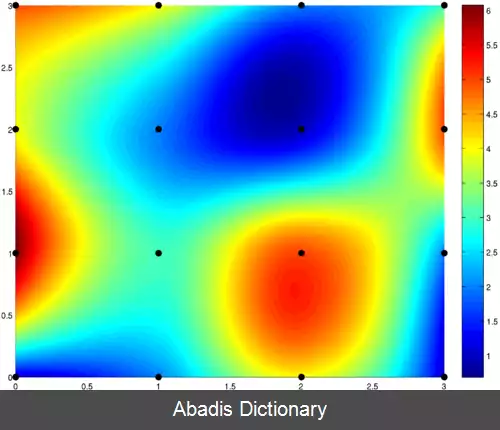
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر کاربردهای پردازش تصویر در صورتی که نیاز به سرعت نباشد به طور معمول از این درونیابی استفاده خواهد. این درونیابی به جای ۴ نقطه درونیابی دوخطی از ۱۶ نقطه همجوار برای انجام درونیابی استفاده می کند.
فرض کنید مقادیر تابع f و مشتقات f x ، f y و f x y در چهار گوشه ( 0 , 0 ) ، ( 1 , 0 ) ، ( 0 , 1 ) و ( 1 , 1 ) مربع واحد مشخص باشد. در این صورت سطح درونیابی شده را می توان نوشت
درونیابی متشکل از مشخص کردن مقادیر ضرایب ناشناخته a i j است. تطبیق p ( x , y ) با مقادیر تابع معادلات زیر را به وجود خواهد آورد:
• f ( 0 , 0 ) = p ( 0 , 0 ) = a 00 {\displaystyle f ( 0, 0 ) =p ( 0, 0 ) =a_{00}}
• f ( 1 , 0 ) = p ( 1 , 0 ) = a 00 + a 10 + a 20 + a 30 {\displaystyle f ( 1, 0 ) =p ( 1, 0 ) =a_{00}+a_{10}+a_{20}+a_{30}}
• f ( 0 , 1 ) = p ( 0 , 1 ) = a 00 + a 01 + a 02 + a 03 {\displaystyle f ( 0, 1 ) =p ( 0, 1 ) =a_{00}+a_{01}+a_{02}+a_{03}}
• f ( 1 , 1 ) = p ( 1 , 1 ) = ∑ i = 0 3 ∑ j = 0 3 a i j {\displaystyle f ( 1, 1 ) =p ( 1, 1 ) =\textstyle \sum _{i=0}^{3}\sum _{j=0}^{3}a_{ij}}
به همین شکل مشتق ها در سمت x و سمت y بدست می آیند:
• f x ( 0 , 0 ) = p x ( 0 , 0 ) = a 10 {\displaystyle f_{x} ( 0, 0 ) =p_{x} ( 0, 0 ) =a_{10}}
• f x ( 1 , 0 ) = p x ( 1 , 0 ) = a 10 + 2 a 20 + 3 a 30 {\displaystyle f_{x} ( 1, 0 ) =p_{x} ( 1, 0 ) =a_{10}+2a_{20}+3a_{30}}
• f x ( 0 , 1 ) = p x ( 0 , 1 ) = a 10 + a 11 + a 12 + a 13 {\displaystyle f_{x} ( 0, 1 ) =p_{x} ( 0, 1 ) =a_{10}+a_{11}+a_{12}+a_{13}}
• f x ( 1 , 1 ) = p x ( 1 , 1 ) = ∑ i = 1 3 ∑ j = 0 3 a i j i {\displaystyle f_{x} ( 1, 1 ) =p_{x} ( 1, 1 ) =\textstyle \sum _{i=1}^{3}\sum _{j=0}^{3}a_{ij}i}
• f y ( 0 , 0 ) = p y ( 0 , 0 ) = a 01 {\displaystyle f_{y} ( 0, 0 ) =p_{y} ( 0, 0 ) =a_{01}}
• f y ( 1 , 0 ) = p y ( 1 , 0 ) = a 01 + a 11 + a 21 + a 31 {\displaystyle f_{y} ( 1, 0 ) =p_{y} ( 1, 0 ) =a_{01}+a_{11}+a_{21}+a_{31}}
• f y ( 0 , 1 ) = p y ( 0 , 1 ) = a 01 + 2 a 02 + 3 a 03 {\displaystyle f_{y} ( 0, 1 ) =p_{y} ( 0, 1 ) =a_{01}+2a_{02}+3a_{03}}
• f y ( 1 , 1 ) = p y ( 1 , 1 ) = ∑ i = 0 3 ∑ j = 1 3 a i j j {\displaystyle f_{y} ( 1, 1 ) =p_{y} ( 1, 1 ) =\textstyle \sum _{i=0}^{3}\sum _{j=1}^{3}a_{ij}j}

wiki: درونیابی دومکعبی
