درخت مستطیلی ( به انگلیسی: R - Tree ) داده ساختاری درختی است که در روش های دسترسی مکانی مانند فهرست کردن اطلاعات چندبعدی همچون مختصات جغرافیایی، مستطیل ها یا چندضلعی ها استفاده می شود. درخت مستطیلی توسط آنتونین گاتمَن ( Antonin Guttman ) در سال 1984[ ۱] پیشنهاد شد و کاربردهای مختلفی در زمینه های نظری و کاربردی بدست آورد. [ ۲] یکی از کاربردهای معمول درخت مستطیلی می تواند ذخیره شیء های مکانی مانند مکان رستوران ها یا چند ضلعی هایی که نقشه های معمولی از آن ها ساخته می شوند: خیابان ها، ساختمان ها، مرز دریاچه ها، خطوط ساحلی و غیره، و سپس یافتن سریع پاسخ سوال هایی مانند "تمام موزه هایی که در ۲ کیلومتری مکان من هستند را پیدا کن"، "بازیابی تمام جاده ها تا ۲ کیلومتری اطراف من ( برای نشان دادن در سامانه راه یابی ) " یا "نزدیک ترین پمپ بنزین را پیدا کن"، باشد.
ایده اصلی این داده ساختار این است که اشیاء نزدیک هم را در یک گروه قرار دهیم و آن ها را با کوچکترین مستطیلی که آن ها را احاطه می کند در سطح بالایی درخت نشان دهیم؛ R در "درخت R" از اول کلمه rectangle گرفته شده است. از آن جایی که همه اشیاء در مستطیل احاطه کننده قرار می گیرند، یک جستجو که تداخلی با مستطیل احاطه کننده ندارد پس نمی تواند تداخلی با هیچ یک از اشیاء داخل آن داشته باشد. در سطح برگ هر مستطیل نشان دهده یک شیء هست؛ در سطوح بالاتر این تعداد افزایش پیدا می کند. این مورد را همچنین می توان به صورت یک تقریب بزرگِ افزاینده از مجموعه داده دید. مشابه با درخت B، درخت مستطیلی هم یک درخت جستجو متوازن است ( پس همهٔ برگ ها در یک ارتفاع هستند ) ، داده ها را در صفحه سازمان دهی می کند، و برای ذخیره بر روی دیسک طراحی شده است. هر صفحه می تواند حاوی یک مقدار حداکثری از ورودی ها باشد که معمولاً با M نشان داده می شود. همچنین یک مقدار حداقلی هم تضمین می شود ( بجز گره ریشه ) ، اگر چه بهترین عملکرد با حداقل پر شدن ۳۰٪ تا ۴۰٪ حداکثر مقدار داده ها، تجربه شده است ( درخت B پر شدن ۵۰٪ و درخت *B پر شدن ۶۶٪ صفحه را ضمانت می کند ) . دلیل این مورد، پیچیده تر بودن متوازن سازی برای داده های مکانی در برابر داده های خطی ذخیره شده در درخت B است. مانند اکثر درخت ها الگوریتم های جستجو ( برای مثال تلاقی، حاوی بودن، جستجو نزدیکترین همسایه ) نسبتاً ساده هستند. ایده اصلی استفاده کردن از مستطیل احاطه کننده برای تصمیم گیری در مورد اینکه داخل یک زیر درخت جستجو شود یا نه، است. به این ترتیب اکثر گره ها در طول جستجو اصلاً دیده نمی شوند. این مورد باعث می شود درخت مستطیلی برای مجموعه داده های بزرگ و پایگاه های داده مناسب باشد؛ جایی که کل درخت در حافظه جا نمی شود و گره ها در هنگام نیاز به حافظه منتقل می شوند. سختی اصلی طراحی درخت مستطیلی این است که از یک طرف درخت باید متوازن باشد ( برگ ها در یک ارتفاع باشند ) و از طرف دیگر مستطیل ها فضای خالی زیادی را پوشش ندهند و زیاد هم پوشانی نداشته باشند ( تا در هنگام جستجو نیاز به بررسی تعداد کمتری زیردرخت باشد ) . برای مثال، ایده اصلی برای اضافه کردن داده ها برای بدست آمدن یک درخت بهینه این است که همیشه به زیردرختی که نیاز به کمترین بزرگ شدن مستطیل احاطه کننده اش دارد، اضافه کنیم. وقتی آن صفحه پر شد، داده ها به دو مجموعه که هر کدام مقدار کمینه ای مساحت را پوشش می دهند، تقسیم می شوند. هدف اکثر تحقیقات و بهبودها برای درخت R، بهبود نحوه ساخت درخت است و می توان آن ها را به دو بخش تقسیم کرد: ساخت یک درخت بهینه از ابتدا ( بارگذاری توده ای ) و ایجاد تغییرات بر روی یک درخت موجود ( حذف و اضافه ) . درخت های مستطیلی کارایی خوب برای بدترین حالت را تضمین نمی کنند ولی عموماً برای داده های واقعی خوب کار می کنند. [ ۳] از جنبه نظری درخت مستطیلی اولویت ( بارگذاری توده ای شده ) از انواع درخت مستطیلی در بدترین حالت بهینه است[ ۴] ، ولی به دلیل زیاد شدن پیچیدگی توجه زیادی در کاربردهای عملی به آن نشده است. وقتی داده ها در درخت مستطیلی سازمان دهی شده اند، k نزدیکترین همسایه های ( برای هر LP - Norm ) همه نقاط می تواند به صورت بهینه با استفاده از یک پیوند زدن مکانی محاسبه شود. [ ۵] این مورد برای بسیاری از الگوریتم های مبتنی بر k نزدیک ترین همسایه ها، مفید است، برای مثال الگوریتم عامل محلی پرت. [ ۶] "تراکم - اتصال - دسته بندی کردن" یک الگوریتم آنالیز خوشه ای است که از ساختار درخت مستطیلی برای انواع مشابه اتصال مکانی استفاده می کند تا به صورت بهینه یک دسته بندی OPTICS را محاسبه کند.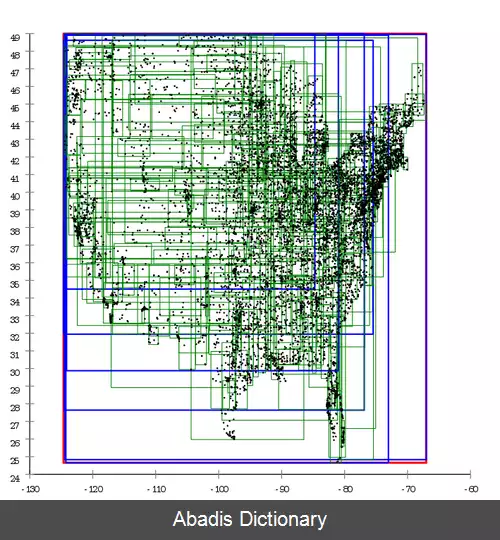
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفایده اصلی این داده ساختار این است که اشیاء نزدیک هم را در یک گروه قرار دهیم و آن ها را با کوچکترین مستطیلی که آن ها را احاطه می کند در سطح بالایی درخت نشان دهیم؛ R در "درخت R" از اول کلمه rectangle گرفته شده است. از آن جایی که همه اشیاء در مستطیل احاطه کننده قرار می گیرند، یک جستجو که تداخلی با مستطیل احاطه کننده ندارد پس نمی تواند تداخلی با هیچ یک از اشیاء داخل آن داشته باشد. در سطح برگ هر مستطیل نشان دهده یک شیء هست؛ در سطوح بالاتر این تعداد افزایش پیدا می کند. این مورد را همچنین می توان به صورت یک تقریب بزرگِ افزاینده از مجموعه داده دید. مشابه با درخت B، درخت مستطیلی هم یک درخت جستجو متوازن است ( پس همهٔ برگ ها در یک ارتفاع هستند ) ، داده ها را در صفحه سازمان دهی می کند، و برای ذخیره بر روی دیسک طراحی شده است. هر صفحه می تواند حاوی یک مقدار حداکثری از ورودی ها باشد که معمولاً با M نشان داده می شود. همچنین یک مقدار حداقلی هم تضمین می شود ( بجز گره ریشه ) ، اگر چه بهترین عملکرد با حداقل پر شدن ۳۰٪ تا ۴۰٪ حداکثر مقدار داده ها، تجربه شده است ( درخت B پر شدن ۵۰٪ و درخت *B پر شدن ۶۶٪ صفحه را ضمانت می کند ) . دلیل این مورد، پیچیده تر بودن متوازن سازی برای داده های مکانی در برابر داده های خطی ذخیره شده در درخت B است. مانند اکثر درخت ها الگوریتم های جستجو ( برای مثال تلاقی، حاوی بودن، جستجو نزدیکترین همسایه ) نسبتاً ساده هستند. ایده اصلی استفاده کردن از مستطیل احاطه کننده برای تصمیم گیری در مورد اینکه داخل یک زیر درخت جستجو شود یا نه، است. به این ترتیب اکثر گره ها در طول جستجو اصلاً دیده نمی شوند. این مورد باعث می شود درخت مستطیلی برای مجموعه داده های بزرگ و پایگاه های داده مناسب باشد؛ جایی که کل درخت در حافظه جا نمی شود و گره ها در هنگام نیاز به حافظه منتقل می شوند. سختی اصلی طراحی درخت مستطیلی این است که از یک طرف درخت باید متوازن باشد ( برگ ها در یک ارتفاع باشند ) و از طرف دیگر مستطیل ها فضای خالی زیادی را پوشش ندهند و زیاد هم پوشانی نداشته باشند ( تا در هنگام جستجو نیاز به بررسی تعداد کمتری زیردرخت باشد ) . برای مثال، ایده اصلی برای اضافه کردن داده ها برای بدست آمدن یک درخت بهینه این است که همیشه به زیردرختی که نیاز به کمترین بزرگ شدن مستطیل احاطه کننده اش دارد، اضافه کنیم. وقتی آن صفحه پر شد، داده ها به دو مجموعه که هر کدام مقدار کمینه ای مساحت را پوشش می دهند، تقسیم می شوند. هدف اکثر تحقیقات و بهبودها برای درخت R، بهبود نحوه ساخت درخت است و می توان آن ها را به دو بخش تقسیم کرد: ساخت یک درخت بهینه از ابتدا ( بارگذاری توده ای ) و ایجاد تغییرات بر روی یک درخت موجود ( حذف و اضافه ) . درخت های مستطیلی کارایی خوب برای بدترین حالت را تضمین نمی کنند ولی عموماً برای داده های واقعی خوب کار می کنند. [ ۳] از جنبه نظری درخت مستطیلی اولویت ( بارگذاری توده ای شده ) از انواع درخت مستطیلی در بدترین حالت بهینه است[ ۴] ، ولی به دلیل زیاد شدن پیچیدگی توجه زیادی در کاربردهای عملی به آن نشده است. وقتی داده ها در درخت مستطیلی سازمان دهی شده اند، k نزدیکترین همسایه های ( برای هر LP - Norm ) همه نقاط می تواند به صورت بهینه با استفاده از یک پیوند زدن مکانی محاسبه شود. [ ۵] این مورد برای بسیاری از الگوریتم های مبتنی بر k نزدیک ترین همسایه ها، مفید است، برای مثال الگوریتم عامل محلی پرت. [ ۶] "تراکم - اتصال - دسته بندی کردن" یک الگوریتم آنالیز خوشه ای است که از ساختار درخت مستطیلی برای انواع مشابه اتصال مکانی استفاده می کند تا به صورت بهینه یک دسته بندی OPTICS را محاسبه کند.

wiki: درخت مستطیلی
