فرض کنید آرایه a به اندازه n که در ابتدا همه مقادیر آن برابر ۰ هستند به ما داده شده است، می خواهیم اعمال زیر را روی این آرایه انجام دهیم:
• به درایه i - ام، x واحد اضافه کن.
• مجموع اعداد درایه i - ام تا درایه j - ام را به دست بیاور.
یک راه حل ساده برای این مسئله با استفاده از آرایه، به این صورت است که دستور ۱ را در ( ۱ ) O و دستور ۲ را در O ( n ) انجام می دهد. پس اگر m دستور داشته باشیم، در بدترین حالت ( زمانی که همه دستورها از نوع دوم باشند ) ، به زمان O ( n ∗ m ) احتیاج داریم. با استفاده از داده ساختار درخت فنویک ( یا درخت اندیس داده شده دودویی ) می توان هر دستور را در O ( l o g n ) و در نتیجه کل دستورها را در O ( m l o g n ) انجام داد. به طور کلی این اعمال توسط درخت بازه ها هم در این زمان انجام می شوند، اما مزیت درخت فنویک در کم بودن حافظه ( دقیقاً به اندازه n ) ، کوتاه بودن کد و همچنین سهولت پیاده سازی آن در ابعاد بیشتر است.
تعریف می کنیم:
• مجموع درایه های اول تا i - ام ( فراوانی تراکمی درایه i - ام ) : c {\displaystyle c}
• مجموع درایه های i - ام تا j - ام: s u m {\displaystyle sum}
این راه حل زمانی که همه دستورهای نوع دوم بعد از دستورها نوع اول باشند، m دستور را در O ( n + m ) انجام می دهد.
به وضوح: s u m = c i − c j − 1
بعد از این که همه دستورها نوع اول، مانند راه قبل در O ( 1 ) انجام شدند، به صورت پویا مقادیر آرایه c را در O ( n ) محاسبه می کنیم. بنابر تعریف c = c + a :c
void initialize ( ) { c = 0; for ( int i=1; i< =n; i++ ) c = c + a; } بعد از این مقدار دهی هم مانند بالا می توانیم مقادیر sum را از روی c به دست بیاوریم. پس کل دستورها را در O ( n + m ) انجام می دهیم. اما اگر دستورها نوع دوم بعد از نوع اول نباشند، بعد از هر دستور نوع اول باید مقادیر آرایه c را به روز کنیم، پس باز هم زمان اجرا در بدترین حالت از O ( n ∗ m ) می شود.
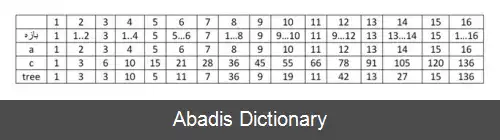
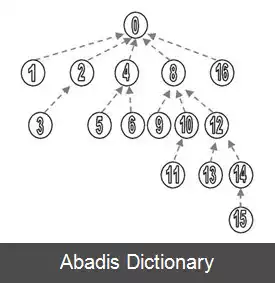
ایده اصلی این درخت این است که هر عدد طبیعی را می توان به صورت جمع تعدادی از توان های ۲ نوشت. به همین ترتیب مجموع یک بازه را می توان به صورت جمع تعدادی زیربازه بدون اشتراک از آن بازه نوشت.
فرض کنید r کوچکترین عددی باشد که بیت r - ام عدد x برابر ۱ باشد. تعریف می کنیم:
t r e e = s u m
t r e e = 0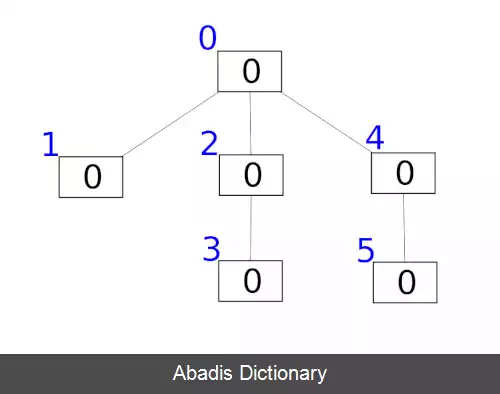
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• به درایه i - ام، x واحد اضافه کن.
• مجموع اعداد درایه i - ام تا درایه j - ام را به دست بیاور.
یک راه حل ساده برای این مسئله با استفاده از آرایه، به این صورت است که دستور ۱ را در ( ۱ ) O و دستور ۲ را در O ( n ) انجام می دهد. پس اگر m دستور داشته باشیم، در بدترین حالت ( زمانی که همه دستورها از نوع دوم باشند ) ، به زمان O ( n ∗ m ) احتیاج داریم. با استفاده از داده ساختار درخت فنویک ( یا درخت اندیس داده شده دودویی ) می توان هر دستور را در O ( l o g n ) و در نتیجه کل دستورها را در O ( m l o g n ) انجام داد. به طور کلی این اعمال توسط درخت بازه ها هم در این زمان انجام می شوند، اما مزیت درخت فنویک در کم بودن حافظه ( دقیقاً به اندازه n ) ، کوتاه بودن کد و همچنین سهولت پیاده سازی آن در ابعاد بیشتر است.
تعریف می کنیم:
• مجموع درایه های اول تا i - ام ( فراوانی تراکمی درایه i - ام ) : c {\displaystyle c}
• مجموع درایه های i - ام تا j - ام: s u m {\displaystyle sum}
این راه حل زمانی که همه دستورهای نوع دوم بعد از دستورها نوع اول باشند، m دستور را در O ( n + m ) انجام می دهد.
به وضوح: s u m = c i − c j − 1
بعد از این که همه دستورها نوع اول، مانند راه قبل در O ( 1 ) انجام شدند، به صورت پویا مقادیر آرایه c را در O ( n ) محاسبه می کنیم. بنابر تعریف c = c + a :c
void initialize ( ) { c = 0; for ( int i=1; i< =n; i++ ) c = c + a; } بعد از این مقدار دهی هم مانند بالا می توانیم مقادیر sum را از روی c به دست بیاوریم. پس کل دستورها را در O ( n + m ) انجام می دهیم. اما اگر دستورها نوع دوم بعد از نوع اول نباشند، بعد از هر دستور نوع اول باید مقادیر آرایه c را به روز کنیم، پس باز هم زمان اجرا در بدترین حالت از O ( n ∗ m ) می شود.
ایده اصلی این درخت این است که هر عدد طبیعی را می توان به صورت جمع تعدادی از توان های ۲ نوشت. به همین ترتیب مجموع یک بازه را می توان به صورت جمع تعدادی زیربازه بدون اشتراک از آن بازه نوشت.
فرض کنید r کوچکترین عددی باشد که بیت r - ام عدد x برابر ۱ باشد. تعریف می کنیم:
t r e e = s u m
t r e e = 0



wiki: درخت فنویک
