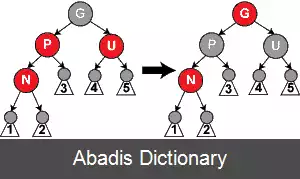
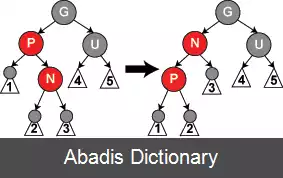
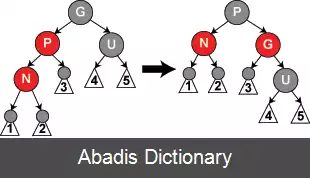
در علم رایانه، ساختمان داده درخت قرمز - سیاه بلوک، یک نوع درخت جستجوی دودویی خود - متوازن است. این ساختمان داده را ابتدا رودولف بایر در سال ۱۹۷۲ با نام «درخت دودویی B متقارن» ابداع کرد ولی نام جدید آن از پایان نامهٔ لیو. جی. گیباس و رابرت سجویک گرفته شده است. این ساختمان داده بسیار پیچیده است با این حال اعمال مربوط به آن حتی در بدترین حالت نیز زمان اجرای خوبی دارند، در واقع زمان جستجو، حذف، و درج برای این درخت مانند درخت AVL لگاریتمی است ( O ( l o g ( n ) ) که n تعداد گره های موجود در درخت است ) . مزیت عمده این ساختمان داده نسبت به درخت AVL این است که اعمال درج و حذف با تنها یک بار پیمایش درخت از بالا به پایین و تغییر رنگ گره ها انجام می شوند و در نتیجه پیاده سازی این درخت از درخت AVL ساده تر است.
درخت قرمز - سیاه یک درخت جستجوی دودویی است که ویژگی های زیر را دارد:
• هر گره با یکی از دو رنگ سیاه یا قرمز رنگ آمیزی می شود.
• ریشه همیشه به رنگ سیاه است.
• اگر گره ای قرمز باشد فرزندان آن باید سیاه باشند.
• تمامی مسیرها از یک گره به برگ ها ( گره های null ) باید دارای تعداد مساوی گره سیاه باشند.
• تمامی برگ ها سیاه هستند. ( برگ گره ای است که فرزندی نداشته باشد - همان گره های null )
ویژگی های بالا موجب این خصوصیت مهم درخت های قرمز - سیاه می شوند:
• اگر یک درخت قرمز سیاه n گره غیر null داشته باشد ارتفاع درخت حداکثر 2 log ( n + 1 ) {\displaystyle 2\log ( n+1 ) } خواهد بود.
ویژگی فوق باعث می شود تا درخت های قرمز - سیاه کارایی مناسبی در اعمال جستجو، درج، و حذف داشته باشند. همچنین به خاطر این که در تمام مسیرهای از ریشه به برگ، تعداد گره های سیاه برابر است ( ویژگی ۴ ) و ممکن نیست دو گره قرمز پشت سر هم قرار بگیرند ( ویژگی ۳ ) ، در این نوع درخت ها طول بلندترین مسیر از ریشه تا برگ هیچ وقت بزرگتر از دو برابر طول کوتاه ترین مسیر ریشه تا برگ نمی شود. با توجه به ویژگی های بالا درخت های قرمز - سیاه ( بر خلاف درخت های جستجوی دودویی معمولی ) هیچ وقت دچار عدم توازن شدید نمی شوند و زمان اجرای لگاریتمی اعمال در این درخت ها تضمین شده است.
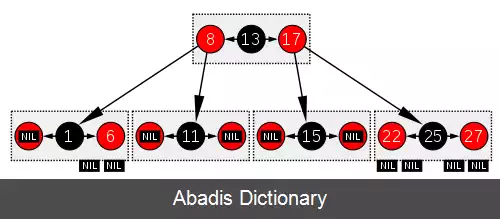
یک درخت قرمز - سیاه ار نظر ساختار شبیه یک درخت بی مرتبه ۴ است که در آن هر گره می تواند ۱ تا ۳ مقدار و همچنین ۲ تا ۴ اشاره گر به فرزندانش داشته باشد. در هر درخت بی، هر گره تنها یک مقدار دارد که برابر مقدار گره سیاه در درخت قرمز - سیاه است، و یک مقدار دلخواه دارد که و/یا بعد از آن در همان گره آمده است، که هر دوی آن ها مساوی گره قرمز در درخت قرمز - سیاه هستند. یک راه دیدن این برابری این است که در گره های قرمز درخت قرمز - سیاه در یک نمایش گرافیکی به سمت بالا حرکت کنیم، به طوری که با پدر سیاهشان در یک ردیف قرار بگیرند و یک دسته افقی را تشکیل دهند. در درخت بی، یا در نمایش گرافیکی تغییر یافته درخت قرمز - سیاه که گفته شد، همه برگ ها عمق یکسانی دارند. در این حالت درخت قرمز - سیاه، از نظر ساختار با درخت بی مرتبه ۴ برابر است که حداقل میزان پرشدن در یک دسته برابر ۳۳٪ است. این نوع درخت بی، عمومی تر از درخت قرمز - سیاه است اما هنگام تبدیل به درخت قرمز - سیاه، ابهاماتی دارد چون از یک درخت بی مرتبه ۴، چندین درخت قرمز - سیاه ساخته می شود. اگر یک دسته در درخت بی تنها ۱ مقدار را شامل شود، این مقدار کمینه است، گره مربوطه سیاه است و دو اشاره گر به فرزندانش دارد. اگر یک دسته شامل ۳ مقدار شود، مقدار وسطی در یک گره سیاه قرار می گیرد و گره های کناری آن باید قرمز باشند. اگر دسته شامل ۲ مقدار باشد، هر کدام از آن ها می تواند در درخت قرمز - سیاه، سیاه باشد و دیگری باید قرمز باشد؛ بنابراین درخت بی مرتبه ۴، مشخص نمی کند که کدامیک از مقادیر در هر دسته ریشه سیاه کل آن دسته و پدر بقیه مقادیر دسته است. با وجود این، عملیات در درخت های قرمز - سیاه از نظر زمان بهینه تر هستند چون نیازی به نگهداشتن برداری از مقادیر نیست. این نگهداری زمانی که مقادیر مستقیماً در هر گره ذخیره شده اند، نسبت به وقتی که تنها مرجع آن ها نگهداری شده است، پر هزینه است. البته گره های درخت بی از نظر حافظه به صرفه تر هستند چون لازم نیست برای آن ها صفت رنگ نگهداری شود. در عوض باید مشخص شود کدام بخش از دسته استفاده شده است. می توان شباهت هایی با درخت های بی مرتبه های بالاتری که از نظر ساختار شبیه درخت دودویی رنگ شده باشند هم ایجاد کرد چون تنها به رنگ های بیشتری نیاز است. مثلاً فرض کنید آبی را هم استفاده کنیم. در نتیجه درخت آبی - قرمز - سیاه مثل درخت قرمز - سیاه تعریف می شود اما با این محدودیت اضافه که دو گره متوالی از نظر مقدار نباید آبی باشند و همه گره های آبی باید فرزندان گره قرمز باشند. چنین درختی معادل یک درخت بی می شود که دسته های آن حداکثر ۷ مقدار و با این رنگ ها دارند :آبی، قرمز، آبی، سیاه، آبی، قرمز، آبی ( هر گروه حداکثر ۱ گره سیاه، ۲ گره قرمز و ۴ گره آبی دارد ) . برای تعدیل کردن حجم مقادیر، درج و حذف در یک درخت دودویی سریعتر از درخت های بی است چون درخت های رنگ شده تلاشی برای بیشینه کردن مقدار پر شدن در یک دسته افقی از گره ها نمی کنند. ( تنها کمینه مقدار پرشدن در درخت های دودویی رنگ شده تضمین شده است ) . چرخش در درخت های بی سریع تر است ( چون چرخش ها اغلب در دسته یکسان رخ می دهند به جای اینکه در چند گره مجزا در یک درخت دودویی رنگ شده انجام شوند ) . با این وجود برای مرتب سازی حجم زیادی از داده ها، درخت های بی بسیار سریعتر هستند چون با گروهی کردن چند فرزند در یک دسته و امکان دسترسی محلی، فشرده تر شده اند. همه بهینه سازی های ممکن در درخت های بی برای افزایش متوسط میزان پرشدن گروه ها در درخت های دودویی رنگ شده هم ممکن است. بیشینه کردن میزان پرشدن در یک درخت بی، مانند کم کردن ارتفاع درخت چند رنگ است که با افزایش تعداد گره های غیر سیاه انجام می شود. بدترین حالت زمانی رخ می دهد که همه گره ها در یک درخت دودویی رنگ شده، سیاه باشند. بهترین حالت زمانی است که تنها یک سوم آن ها سیاه باشند ( و دو سوم بقیه، قرمز باشند ) .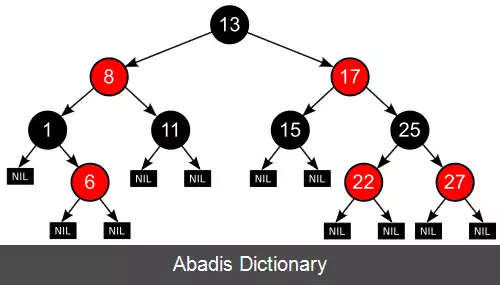
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرخت قرمز - سیاه یک درخت جستجوی دودویی است که ویژگی های زیر را دارد:
• هر گره با یکی از دو رنگ سیاه یا قرمز رنگ آمیزی می شود.
• ریشه همیشه به رنگ سیاه است.
• اگر گره ای قرمز باشد فرزندان آن باید سیاه باشند.
• تمامی مسیرها از یک گره به برگ ها ( گره های null ) باید دارای تعداد مساوی گره سیاه باشند.
• تمامی برگ ها سیاه هستند. ( برگ گره ای است که فرزندی نداشته باشد - همان گره های null )
ویژگی های بالا موجب این خصوصیت مهم درخت های قرمز - سیاه می شوند:
• اگر یک درخت قرمز سیاه n گره غیر null داشته باشد ارتفاع درخت حداکثر 2 log ( n + 1 ) {\displaystyle 2\log ( n+1 ) } خواهد بود.
ویژگی فوق باعث می شود تا درخت های قرمز - سیاه کارایی مناسبی در اعمال جستجو، درج، و حذف داشته باشند. همچنین به خاطر این که در تمام مسیرهای از ریشه به برگ، تعداد گره های سیاه برابر است ( ویژگی ۴ ) و ممکن نیست دو گره قرمز پشت سر هم قرار بگیرند ( ویژگی ۳ ) ، در این نوع درخت ها طول بلندترین مسیر از ریشه تا برگ هیچ وقت بزرگتر از دو برابر طول کوتاه ترین مسیر ریشه تا برگ نمی شود. با توجه به ویژگی های بالا درخت های قرمز - سیاه ( بر خلاف درخت های جستجوی دودویی معمولی ) هیچ وقت دچار عدم توازن شدید نمی شوند و زمان اجرای لگاریتمی اعمال در این درخت ها تضمین شده است.
یک درخت قرمز - سیاه ار نظر ساختار شبیه یک درخت بی مرتبه ۴ است که در آن هر گره می تواند ۱ تا ۳ مقدار و همچنین ۲ تا ۴ اشاره گر به فرزندانش داشته باشد. در هر درخت بی، هر گره تنها یک مقدار دارد که برابر مقدار گره سیاه در درخت قرمز - سیاه است، و یک مقدار دلخواه دارد که و/یا بعد از آن در همان گره آمده است، که هر دوی آن ها مساوی گره قرمز در درخت قرمز - سیاه هستند. یک راه دیدن این برابری این است که در گره های قرمز درخت قرمز - سیاه در یک نمایش گرافیکی به سمت بالا حرکت کنیم، به طوری که با پدر سیاهشان در یک ردیف قرار بگیرند و یک دسته افقی را تشکیل دهند. در درخت بی، یا در نمایش گرافیکی تغییر یافته درخت قرمز - سیاه که گفته شد، همه برگ ها عمق یکسانی دارند. در این حالت درخت قرمز - سیاه، از نظر ساختار با درخت بی مرتبه ۴ برابر است که حداقل میزان پرشدن در یک دسته برابر ۳۳٪ است. این نوع درخت بی، عمومی تر از درخت قرمز - سیاه است اما هنگام تبدیل به درخت قرمز - سیاه، ابهاماتی دارد چون از یک درخت بی مرتبه ۴، چندین درخت قرمز - سیاه ساخته می شود. اگر یک دسته در درخت بی تنها ۱ مقدار را شامل شود، این مقدار کمینه است، گره مربوطه سیاه است و دو اشاره گر به فرزندانش دارد. اگر یک دسته شامل ۳ مقدار شود، مقدار وسطی در یک گره سیاه قرار می گیرد و گره های کناری آن باید قرمز باشند. اگر دسته شامل ۲ مقدار باشد، هر کدام از آن ها می تواند در درخت قرمز - سیاه، سیاه باشد و دیگری باید قرمز باشد؛ بنابراین درخت بی مرتبه ۴، مشخص نمی کند که کدامیک از مقادیر در هر دسته ریشه سیاه کل آن دسته و پدر بقیه مقادیر دسته است. با وجود این، عملیات در درخت های قرمز - سیاه از نظر زمان بهینه تر هستند چون نیازی به نگهداشتن برداری از مقادیر نیست. این نگهداری زمانی که مقادیر مستقیماً در هر گره ذخیره شده اند، نسبت به وقتی که تنها مرجع آن ها نگهداری شده است، پر هزینه است. البته گره های درخت بی از نظر حافظه به صرفه تر هستند چون لازم نیست برای آن ها صفت رنگ نگهداری شود. در عوض باید مشخص شود کدام بخش از دسته استفاده شده است. می توان شباهت هایی با درخت های بی مرتبه های بالاتری که از نظر ساختار شبیه درخت دودویی رنگ شده باشند هم ایجاد کرد چون تنها به رنگ های بیشتری نیاز است. مثلاً فرض کنید آبی را هم استفاده کنیم. در نتیجه درخت آبی - قرمز - سیاه مثل درخت قرمز - سیاه تعریف می شود اما با این محدودیت اضافه که دو گره متوالی از نظر مقدار نباید آبی باشند و همه گره های آبی باید فرزندان گره قرمز باشند. چنین درختی معادل یک درخت بی می شود که دسته های آن حداکثر ۷ مقدار و با این رنگ ها دارند :آبی، قرمز، آبی، سیاه، آبی، قرمز، آبی ( هر گروه حداکثر ۱ گره سیاه، ۲ گره قرمز و ۴ گره آبی دارد ) . برای تعدیل کردن حجم مقادیر، درج و حذف در یک درخت دودویی سریعتر از درخت های بی است چون درخت های رنگ شده تلاشی برای بیشینه کردن مقدار پر شدن در یک دسته افقی از گره ها نمی کنند. ( تنها کمینه مقدار پرشدن در درخت های دودویی رنگ شده تضمین شده است ) . چرخش در درخت های بی سریع تر است ( چون چرخش ها اغلب در دسته یکسان رخ می دهند به جای اینکه در چند گره مجزا در یک درخت دودویی رنگ شده انجام شوند ) . با این وجود برای مرتب سازی حجم زیادی از داده ها، درخت های بی بسیار سریعتر هستند چون با گروهی کردن چند فرزند در یک دسته و امکان دسترسی محلی، فشرده تر شده اند. همه بهینه سازی های ممکن در درخت های بی برای افزایش متوسط میزان پرشدن گروه ها در درخت های دودویی رنگ شده هم ممکن است. بیشینه کردن میزان پرشدن در یک درخت بی، مانند کم کردن ارتفاع درخت چند رنگ است که با افزایش تعداد گره های غیر سیاه انجام می شود. بدترین حالت زمانی رخ می دهد که همه گره ها در یک درخت دودویی رنگ شده، سیاه باشند. بهترین حالت زمانی است که تنها یک سوم آن ها سیاه باشند ( و دو سوم بقیه، قرمز باشند ) .





wiki: درخت سرخ سیاه
