درخت آآ. یک درخت AA در علوم کامپیوتر، نوعی از درخت جستجوی دودویی خود متوازن است که مورد استفاده آن در ذخیره سازی و بازیابی اطلاعات مرتب شده، به صورت بهینه و مناسب است. دلیل نامگذاری درخت AA، کاشفان آن، یعنی Arne Andersson می باشد. درخت های AA یک نوع درخت سرخ - سیاه ( red - black ) هستند، که به نوبه خود تعمیمی بر درخت جستجوی دودویی محسوب می شوند. برخلاف درختان سرخ - سیاه ( red - black ) ، در درخت AA، گره های قرمز فقط می توانند به عنوان فرزند سمت راست اضافه شوند. به عبارت دیگر هیچ گره قرمزی نمی تواند به عنوان فرزند سمت چپ انتخاب شود. این باعث می شود که در شبیه سازی یک درخت ۲ - ۳ به جای یک درخت ۴ - ۳ - ۲، در ساده سازی عملیات های نگهداری بسیار کمک کند. الگوریتم های نگهداری برای یک درخت سرخ - سیاه ( red - black ) به هفت شکل متفاوت زیر، برای متعادل نگه کردن درخت، در نظر گرفته می شوند:
در صورتی که در یک درخت AA، فقط کافی است که به دو شکل زیر در نظر گرفته شود و علت آن هم این است که تنها لینک های سمت راست می توانند به رنگ قرمز باشند:
از آنجایی که درخت های سرخ - سیاه به یک بیت از فراداده های هر گره ( رنگ ) برای متعادل ساز ی نیاز دارند، درخت های AA به پیچیدگی محاسباتی log N بیت از فراداده های هر گره نیاز دارد، به صورت یک عدد طبیعی به نام «سطح». یک درخت AA دارای ویژگی های زیر است:
• سطح هر برگ برابر یک است.
• سطح هر فرزند سمت چپ دقیقاً یکی کمتر از والد خود است.
• سطح هر فرزند سمت راست، برابر یا یکی کمتر از والد خود است.
• سطح هر نوه سمت راست، اکیداً کمتر از جد خود است.
• هر گره از سطح بیشتر از یک دو فرزند دارد.
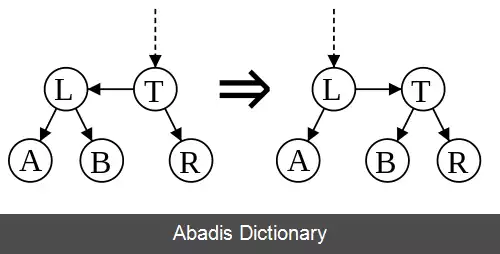
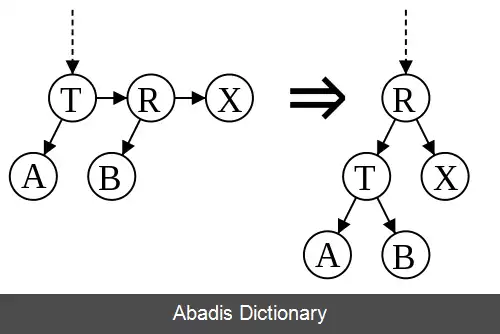
لینکی ( یال ) که در آن سطح یک فرزند با سطح والد خود برابر باشد را لینک ( یال ) افقی می نامند و مشابه آن لینک قرمز در درخت سرخ - سیاه است. تک یال های افقی به سمت راست مجاز ولی یال های متوالی غیرمجاز هستند. این ها محدودیت های بیشتری ( در درخت AA ) هستند از محدودیت های مشابه، در درخت سرخ - سیاه، با این نتیجه که متعادل سازی مجدد یک درخت AA بسیار ساده تر از درخت سرخ - سیاه است. درج کردن و حذف کردن در درخت AA به صورت موقتی آن را نامتعادل می کند ( که باعث می شود با ویژگی های آن در تضاد باشد ) . تنها دو عملیات مجزا نیاز است تا درخت را مجدداً متعادل سازیم: “skew” ( مورب ) و ”split” ( شکاف ) . مورب ( skew ) یک دوران به سمت راست است که منجر به جایگزاری یک زیر درخت، شامل یک یال افقی به سمت چپ، با، یک زیر درخت، شامل یک یال افقی به سمت راست، می شود. شکاف ( split ) یک دوران به سمت چپ و افزاینده سطح است که یک زیر درخت، شامل دو یا بیشتر از دو یال افقی متوالی به سمت راست، را با یک زیر درخت، شامل دو یا کمتر از دو یال افقی متوالی به سمت راست، جایگزین می کند. پیاده سازی «متعادل نگه داشتن» درج کردن و حذف کردن، توسط عملگرهای مورب ( skew ) و شکاف ( split ) ساده سازی شده است، تا فقط در صورت نیاز اصلاح درخت صورت گیرد، به جای اینکه صدا زننده های آن انتخاب کنند که مورب صورت بگیرد یا شکاف.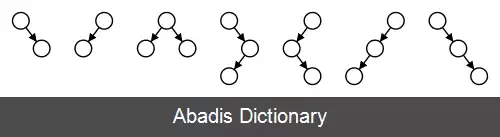
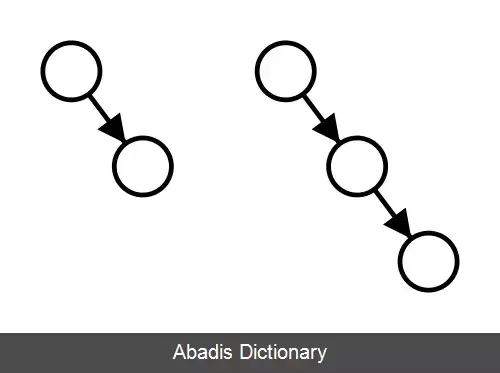
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر صورتی که در یک درخت AA، فقط کافی است که به دو شکل زیر در نظر گرفته شود و علت آن هم این است که تنها لینک های سمت راست می توانند به رنگ قرمز باشند:
از آنجایی که درخت های سرخ - سیاه به یک بیت از فراداده های هر گره ( رنگ ) برای متعادل ساز ی نیاز دارند، درخت های AA به پیچیدگی محاسباتی log N بیت از فراداده های هر گره نیاز دارد، به صورت یک عدد طبیعی به نام «سطح». یک درخت AA دارای ویژگی های زیر است:
• سطح هر برگ برابر یک است.
• سطح هر فرزند سمت چپ دقیقاً یکی کمتر از والد خود است.
• سطح هر فرزند سمت راست، برابر یا یکی کمتر از والد خود است.
• سطح هر نوه سمت راست، اکیداً کمتر از جد خود است.
• هر گره از سطح بیشتر از یک دو فرزند دارد.
لینکی ( یال ) که در آن سطح یک فرزند با سطح والد خود برابر باشد را لینک ( یال ) افقی می نامند و مشابه آن لینک قرمز در درخت سرخ - سیاه است. تک یال های افقی به سمت راست مجاز ولی یال های متوالی غیرمجاز هستند. این ها محدودیت های بیشتری ( در درخت AA ) هستند از محدودیت های مشابه، در درخت سرخ - سیاه، با این نتیجه که متعادل سازی مجدد یک درخت AA بسیار ساده تر از درخت سرخ - سیاه است. درج کردن و حذف کردن در درخت AA به صورت موقتی آن را نامتعادل می کند ( که باعث می شود با ویژگی های آن در تضاد باشد ) . تنها دو عملیات مجزا نیاز است تا درخت را مجدداً متعادل سازیم: “skew” ( مورب ) و ”split” ( شکاف ) . مورب ( skew ) یک دوران به سمت راست است که منجر به جایگزاری یک زیر درخت، شامل یک یال افقی به سمت چپ، با، یک زیر درخت، شامل یک یال افقی به سمت راست، می شود. شکاف ( split ) یک دوران به سمت چپ و افزاینده سطح است که یک زیر درخت، شامل دو یا بیشتر از دو یال افقی متوالی به سمت راست، را با یک زیر درخت، شامل دو یا کمتر از دو یال افقی متوالی به سمت راست، جایگزین می کند. پیاده سازی «متعادل نگه داشتن» درج کردن و حذف کردن، توسط عملگرهای مورب ( skew ) و شکاف ( split ) ساده سازی شده است، تا فقط در صورت نیاز اصلاح درخت صورت گیرد، به جای اینکه صدا زننده های آن انتخاب کنند که مورب صورت بگیرد یا شکاف.




wiki: درخت آآ
