دایره واحد، دایره ای به شعاع واحد است. معمولاً و به خصوص در مثلثات، دایرهٔ واحد دایره ای است با شعاعی به طول ۱ که مرکز آن نقطهٔ ( ۰، ۰ ) در دستگاه مختصات دکارتی در صفحه اقلیدسی است. با استفاده از این دایره ی ساده می توان نسبت های مثلثاتی را به بدست آورد.
اگر ( x٫y ) نقطه ای بر روی دایره واحد در ربع اول باشد آنگاه x و y طول ضلع های مثلث قائم الزاویه با وتری به طول یک هستند؛ بنابراین بر اساس قضیه فیثاغورس، x و y در معادلهٔ x 2 + y 2 = 1 صدق می کنند. این معادله، معادلهٔ دایره ای به شعاع ۱ و مرکز مبدأ مختصات است که هر نقطه ای روی دایرهٔ واحد در آن صدق می کند.
هم چنین با استفاده از مفهوم دایره ی مثلثاتی می توان طول ها و زوایا را در اشکال هندسی بدست آورد.
• صورت نمایی:
• صورت مثلثاتی:
θ زاویه ای است که خط گذرنده از Z و مبدأ مختصات با جهت مثبت محور Xها می سازد.
جهت مثبت دایره مثلثاتی را مخالف جهت حرکت عقربه های ساعت در نظر می گیرند. [ ۱]
نقطه ای مانند A با مختصات ( cos θ , sin θ ) بر روی محیط دایره در نظر بگیرید ( شکل روبرو ) . طبق تعاریف سینوس و کسینوس می دانیم که cos ( θ ) = x و sin ( θ ) = y . از طرفی برای مثلث قائم الزاویه O A C که وتر آن یک واحد است، داریم cos 2 ( θ ) + sin 2 ( θ ) = 1 که این رابطه یکی از پایه ای ترین مفاهیم مثلثات است.
با توجه به خواص دایره مثلثاتی و از آنجا که توابع سینوس و کسینوس متناوب هستند خواهیم داشت:
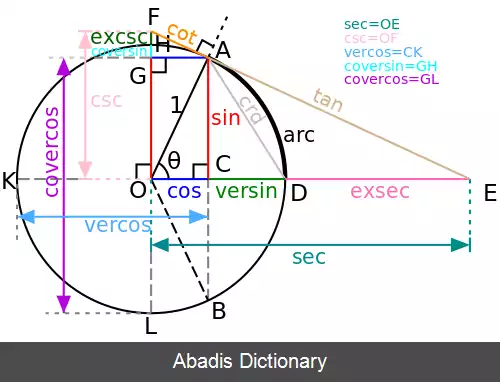
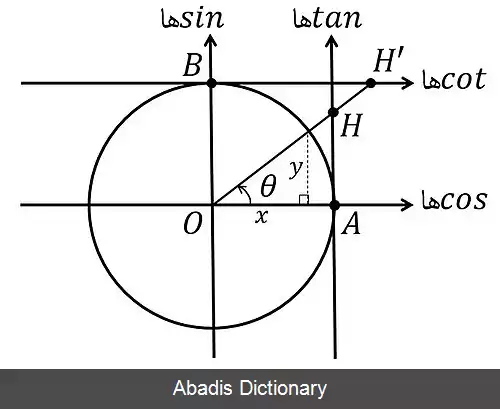
در دایره مثلثاتی با شناخت محورها و رسم آن ها به راحتی می توانیم مقادیر زوایای مختلف و علامت آن ها را پیدا کنیم. در دایره مثلثاتی محور طول ها محور کسینوس ها نامیده می شود و محور عرض ها محور سینوس ها. اگر از سمت راست و از فاصله یک واحدی مرکز دایره مثلثاتی ( نقطه A در شکل روبه رو ) خطی به موازات محور سینوس ها رسم کنیم، این خط محور تانژانت ها نامیده خواهد شد. همچنین اگر از سمت فوقانی و فاصله یک واحدی مرکز دایره مثلثاتی ( از نقطهٔ B در شکل رو به رو ) خطی به موازات محور کسینوس ها رسم کنیم این محور، محور کتانژانت ها نام دارد. سمت راست محور کسینوس ها و محور کتانژانت ها مثبت و سمت چپ منفی می باشد. اگر زاویهٔ مورد نظر را داشته باشیم، و از ضلع انتهایی به این محورها وصل کنیم، علامت و مقدار آن ها مشخص می شود. [ ۲]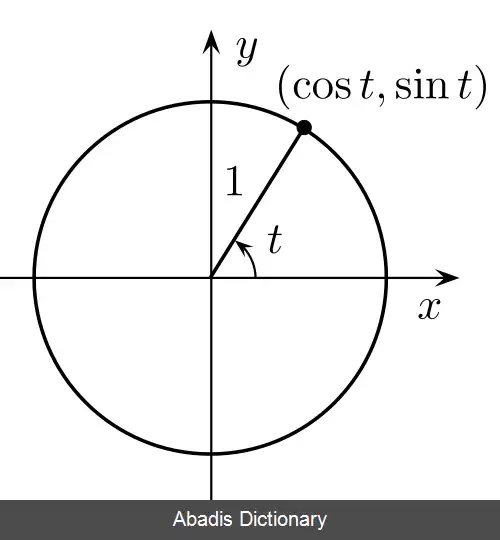
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر ( x٫y ) نقطه ای بر روی دایره واحد در ربع اول باشد آنگاه x و y طول ضلع های مثلث قائم الزاویه با وتری به طول یک هستند؛ بنابراین بر اساس قضیه فیثاغورس، x و y در معادلهٔ x 2 + y 2 = 1 صدق می کنند. این معادله، معادلهٔ دایره ای به شعاع ۱ و مرکز مبدأ مختصات است که هر نقطه ای روی دایرهٔ واحد در آن صدق می کند.
هم چنین با استفاده از مفهوم دایره ی مثلثاتی می توان طول ها و زوایا را در اشکال هندسی بدست آورد.
• صورت نمایی:
• صورت مثلثاتی:
θ زاویه ای است که خط گذرنده از Z و مبدأ مختصات با جهت مثبت محور Xها می سازد.
جهت مثبت دایره مثلثاتی را مخالف جهت حرکت عقربه های ساعت در نظر می گیرند. [ ۱]
نقطه ای مانند A با مختصات ( cos θ , sin θ ) بر روی محیط دایره در نظر بگیرید ( شکل روبرو ) . طبق تعاریف سینوس و کسینوس می دانیم که cos ( θ ) = x و sin ( θ ) = y . از طرفی برای مثلث قائم الزاویه O A C که وتر آن یک واحد است، داریم cos 2 ( θ ) + sin 2 ( θ ) = 1 که این رابطه یکی از پایه ای ترین مفاهیم مثلثات است.
با توجه به خواص دایره مثلثاتی و از آنجا که توابع سینوس و کسینوس متناوب هستند خواهیم داشت:
در دایره مثلثاتی با شناخت محورها و رسم آن ها به راحتی می توانیم مقادیر زوایای مختلف و علامت آن ها را پیدا کنیم. در دایره مثلثاتی محور طول ها محور کسینوس ها نامیده می شود و محور عرض ها محور سینوس ها. اگر از سمت راست و از فاصله یک واحدی مرکز دایره مثلثاتی ( نقطه A در شکل روبه رو ) خطی به موازات محور سینوس ها رسم کنیم، این خط محور تانژانت ها نامیده خواهد شد. همچنین اگر از سمت فوقانی و فاصله یک واحدی مرکز دایره مثلثاتی ( از نقطهٔ B در شکل رو به رو ) خطی به موازات محور کسینوس ها رسم کنیم این محور، محور کتانژانت ها نام دارد. سمت راست محور کسینوس ها و محور کتانژانت ها مثبت و سمت چپ منفی می باشد. اگر زاویهٔ مورد نظر را داشته باشیم، و از ضلع انتهایی به این محورها وصل کنیم، علامت و مقدار آن ها مشخص می شود. [ ۲]



wiki: دایره واحد
