در هندسه، دایرهٔ نُه نقطه ( که به دایره اویلر نیز معروف است ) دایرهای است که می توان آن را برای هر مثلثی ایجاد کرد. علت نام گذاری این دایره به این نام، این است که از ۹ نقطهٔ مهم مثلث می گذرد. این ۹ نقطه ( هر مورد شامل ۳ نقطه است ) :
• میانه های اضلاع مثلث
• پای ارتفاع ها
• وسط پاره خطهایی که از هر رأس تا مرکز ارتفاعی ( Orthocenter ) مثلث کشیده شده اند.
هستند. [ ۱]
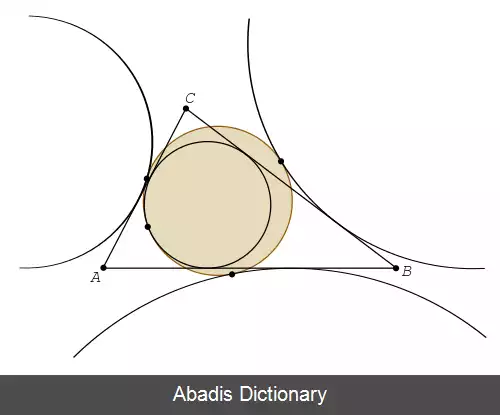
هم چنین دایرهٔ نه نقطه با نام های دایرهٔ فوئرباخ، دایرهٔ ترکوئم، دایرهٔ اویلر، دایرهٔ دوازده نقطه، دایرهٔ ۶ نقطه، دایرهٔ n نقطه و دایره اوساط نیز شناخته می شود. دایره نه نقطه با دایره محاطی مثلث در نقطه ای به نام فوئرباخ مماس است. [ ۲]
کارل ویلهلم فوئرباخ ریاضیدان آلمانی برای نخستین بار ویژگی های دایره ۶ نقطه ای را توصیف کرد که از پای عمودها و از وسط اضلاع مثلث می گذرد. لیکن ریاضیدان فرانسوی Olry Terquem برای اولین بار شرح کاملی از ۹ نقطه این دایره داد.
• شعاع دایره اویلر هر مثلث برابر با نصف شعاع دایره محیطی آن مثلث است.
• مرکز دایره اویلر در مرکز خطی است که مرکز دایره محیطی را به مرکز ارتفاعی مثلث متصل می کند.
• مرکز دایره اویلر بر خط اویلر واقع است. ( خط اویلر خطی است که از مرکز ثقل مثلث ، مرکز ارتفاعی مثلث و مرکز دایره محیطی مثلث عبور می کند
• طبق قضیه فوئرباخ ( Feuerbach ) ، دایره اویلر بر دایره های محاطی داخلی و خارجی مثلث مماس است
• اگر از مرکز ارتفاعی مثلث ( نقطه H ) خطی رسم کنیم تا دایره محیطی را در نقطه X و دایره اویلر را در نقطه Y قطع کند. همواره داریم XY = HY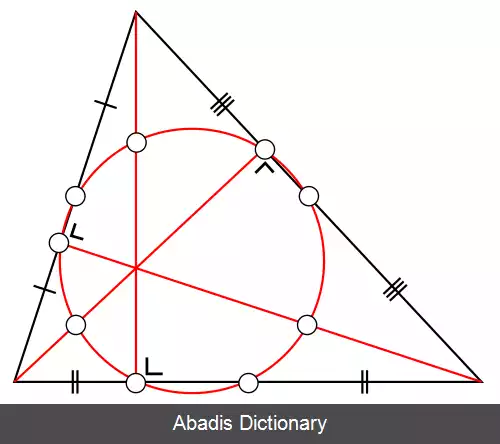
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• میانه های اضلاع مثلث
• پای ارتفاع ها
• وسط پاره خطهایی که از هر رأس تا مرکز ارتفاعی ( Orthocenter ) مثلث کشیده شده اند.
هستند. [ ۱]
هم چنین دایرهٔ نه نقطه با نام های دایرهٔ فوئرباخ، دایرهٔ ترکوئم، دایرهٔ اویلر، دایرهٔ دوازده نقطه، دایرهٔ ۶ نقطه، دایرهٔ n نقطه و دایره اوساط نیز شناخته می شود. دایره نه نقطه با دایره محاطی مثلث در نقطه ای به نام فوئرباخ مماس است. [ ۲]
کارل ویلهلم فوئرباخ ریاضیدان آلمانی برای نخستین بار ویژگی های دایره ۶ نقطه ای را توصیف کرد که از پای عمودها و از وسط اضلاع مثلث می گذرد. لیکن ریاضیدان فرانسوی Olry Terquem برای اولین بار شرح کاملی از ۹ نقطه این دایره داد.
• شعاع دایره اویلر هر مثلث برابر با نصف شعاع دایره محیطی آن مثلث است.
• مرکز دایره اویلر در مرکز خطی است که مرکز دایره محیطی را به مرکز ارتفاعی مثلث متصل می کند.
• مرکز دایره اویلر بر خط اویلر واقع است. ( خط اویلر خطی است که از مرکز ثقل مثلث ، مرکز ارتفاعی مثلث و مرکز دایره محیطی مثلث عبور می کند
• طبق قضیه فوئرباخ ( Feuerbach ) ، دایره اویلر بر دایره های محاطی داخلی و خارجی مثلث مماس است
• اگر از مرکز ارتفاعی مثلث ( نقطه H ) خطی رسم کنیم تا دایره محیطی را در نقطه X و دایره اویلر را در نقطه Y قطع کند. همواره داریم XY = HY


wiki: دایره نه نقطه
