خودهمبستگی
فرهنگستان زبان و ادب
دانشنامه عمومی
خودهمبستگی[ ۱] ( به انگلیسی: autocorrelation ) ، همبستگیِ متقابلِ سیگنال ( داده ها ) با خودش است. به طور غیررسمی، خودهمبستگی، همسانیِ ( شباهت ) سیگنال ( داده ها ) با نسخهٔ شیفت یافتهٔ خود است.
خودهمبستگی، ابزاری ریاضی برای یافتن الگوهای تکراری ( مانند حضور یک سیگنال متناوب در نویز ) ، یا شناسایی یک فرکانس مشخص در سیگنالی دارای فرکانس های هارمونیک است. از خودهمبستگی، اغلب در پردازش سیگنال برای تحلیل توابع یا داده ها از جمله تحلیل حوزه زمان سیگنال ها استفاده می شود.
در آمار، خودهمبستگی یک فرایند تصادفی، همبستگیِ مقادیر فرایند در زمان های مختلف را به عنوان تابعی دو - متغیّره ( زمان و شیفت زمانی ) ، یا تابعی تک متغیّره ( شیفت زمانی ) توصیف می کند. اگر X فرایندی تکرارپذیر باشد و i نقطه ای از زمان بعد از آغاز فرایند ( i عددی صحیح برای فرایند زمان گسسته یا عددی حقیقی برای فرایند زمان پیوسته ) است؛ بنابراین Xi مقدار ( یا تحقق ) فرایند در زمان i است.
فرض کنیم فرایند، با میانگین μi و واریانس σ۲i برای همه زمان های i تعریف شده است. خودهمبستگی فرایند در دو زمان s و t عبارت است از:
که E عملگر امید ریاضی است. این بیان برای همه فرایندها یا سری های زمانی، خوش تعریف نیست، چون ممکن است واریانس برابر صفر ( برای یک فرایند ثابت ) یا بینهایت باشد. اگر تابع R خوش تعریف باشد، مقدار آن باید در محدوده قرار گیرد، که ۱ نشان دهنده همبستگی کامل و ۱ - نشان دهنده ضدهمبستگی کامل است. اگر Xt یک فرایند ایستا ( به انگلیسی: Stationary ) باشد، میانگین μ و واریانس σ۲ مستقل از زمان هستند و خودهمبستگی فقط به تفاضل t و s بستگی دارد نه به مقدار مطلق آن ها. این موضوع بیان می کند که خودهمبستگی یک فرایند ایستا می تواند به عنوان تابعی از تأخیر ( شیفت ) زمانی بیان شود، و همچنین باید یک تابع زوج از τ = s − t باشد.
و با توجه به زوج بودن این تابع، می توانیم بگوییم:
این عمل مشترک در برخی رشته ها به غیر از آمار و تحلیل سری های زمانی، برای نرمال کردن به وسیله σ۲ و استفاده از «خودهمبستگی» مترادف با «اتو کوواریانس» است. به هر حال، نرمال کردن به دو دلیل اهمیت دارد: به علت تفسیر خودهمبستگی به عنوان یک همبستگی که مقدار بدون مقیاس «قدرت وابستگی آماری» را فراهم می کند و چون نرمال کردن روی خصوصیات آماری خودهمبستگی های برآورد شده مؤثر است.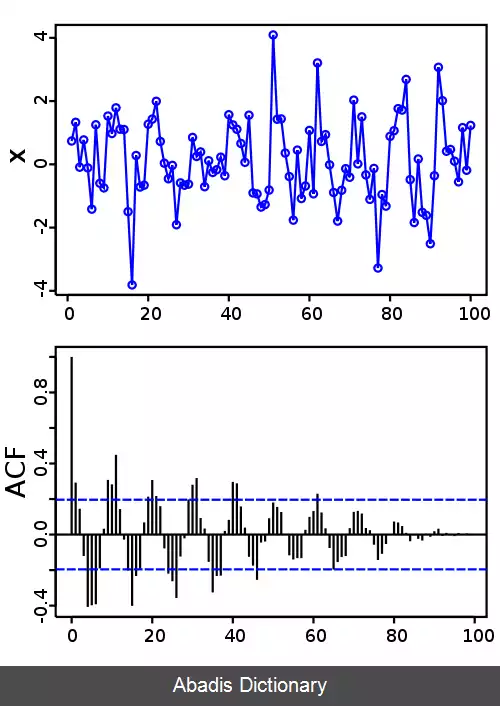
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفخودهمبستگی، ابزاری ریاضی برای یافتن الگوهای تکراری ( مانند حضور یک سیگنال متناوب در نویز ) ، یا شناسایی یک فرکانس مشخص در سیگنالی دارای فرکانس های هارمونیک است. از خودهمبستگی، اغلب در پردازش سیگنال برای تحلیل توابع یا داده ها از جمله تحلیل حوزه زمان سیگنال ها استفاده می شود.
در آمار، خودهمبستگی یک فرایند تصادفی، همبستگیِ مقادیر فرایند در زمان های مختلف را به عنوان تابعی دو - متغیّره ( زمان و شیفت زمانی ) ، یا تابعی تک متغیّره ( شیفت زمانی ) توصیف می کند. اگر X فرایندی تکرارپذیر باشد و i نقطه ای از زمان بعد از آغاز فرایند ( i عددی صحیح برای فرایند زمان گسسته یا عددی حقیقی برای فرایند زمان پیوسته ) است؛ بنابراین Xi مقدار ( یا تحقق ) فرایند در زمان i است.
فرض کنیم فرایند، با میانگین μi و واریانس σ۲i برای همه زمان های i تعریف شده است. خودهمبستگی فرایند در دو زمان s و t عبارت است از:
که E عملگر امید ریاضی است. این بیان برای همه فرایندها یا سری های زمانی، خوش تعریف نیست، چون ممکن است واریانس برابر صفر ( برای یک فرایند ثابت ) یا بینهایت باشد. اگر تابع R خوش تعریف باشد، مقدار آن باید در محدوده قرار گیرد، که ۱ نشان دهنده همبستگی کامل و ۱ - نشان دهنده ضدهمبستگی کامل است. اگر Xt یک فرایند ایستا ( به انگلیسی: Stationary ) باشد، میانگین μ و واریانس σ۲ مستقل از زمان هستند و خودهمبستگی فقط به تفاضل t و s بستگی دارد نه به مقدار مطلق آن ها. این موضوع بیان می کند که خودهمبستگی یک فرایند ایستا می تواند به عنوان تابعی از تأخیر ( شیفت ) زمانی بیان شود، و همچنین باید یک تابع زوج از τ = s − t باشد.
و با توجه به زوج بودن این تابع، می توانیم بگوییم:
این عمل مشترک در برخی رشته ها به غیر از آمار و تحلیل سری های زمانی، برای نرمال کردن به وسیله σ۲ و استفاده از «خودهمبستگی» مترادف با «اتو کوواریانس» است. به هر حال، نرمال کردن به دو دلیل اهمیت دارد: به علت تفسیر خودهمبستگی به عنوان یک همبستگی که مقدار بدون مقیاس «قدرت وابستگی آماری» را فراهم می کند و چون نرمال کردن روی خصوصیات آماری خودهمبستگی های برآورد شده مؤثر است.

wiki: خودهمبستگی
