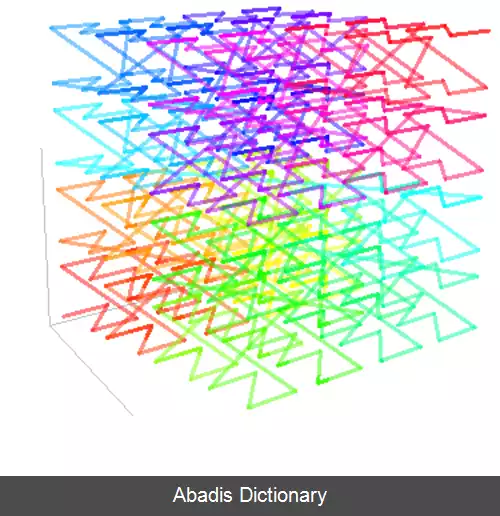
در آنالیز ریاضی و علوم رایانه، توابع ای مانند مرتبه Z، منحنی Lebesgue، منحنی پر کردن فضای مورتون، [ ۱] مرتبه مورتون یا کد مورتون داده های چند بعدی را در یک بعد حفظ کرده و در عین حال محلی از نقاط داده را حفظ می کنند. این نام از گای مک دونالد مورتون گرفته شده است که برای اولین بار دستور ترتیب دهی فایل ها را در سال ۱۹۶۶ داد. [ ۲] مقدار z یک نقطه در چند بعد به سادگی با در هم آمیختن مقادیر دودویی مختصات آن محاسبه می شود. پس از طبقه بندی داده ها به این ترتیب، می توان از هر داده ساختار یک بعدی مانند درخت جستجوی دودویی، درختان B، لیست پرشی یا جدول های درهمسازی استفاده کرد. ترتیب حاصل معادل ترتیب بدست آمده از عمق اول یک چاردرخت توصیف می شود.
جدول زیر مقادیر Z را در دو بعد نشان می دهد که ۰ ≤ x ≤ ۷، ۰ ≤ y ≤ ۷ است ( هم در مبنای ۱۰ و هم به صورت دودویی نشان داده می شود ) در هم آمیختن مقادیر مختصات باینری مقادیر باینری z را بازمی گرداند. متصل کردن مقادیر z به ترتیب عددی آن ها یک خم بازگشتی Z شکل را می سازد.
مقادیر Z از xها به عنوان اعداد باینری از دنبالهٔ Moser–de Bruijn در نظر گرفته می شوند و فقط در موقعیت های مساوی خود دارای بیت های غیرصفر هستند:
{x = {0b000000, 0b000001, 0b000100, 0b000101, 0b010000, 0b010001, 0b010100, 0b010101 مجموع و تفاوت دو x با استفاده از عملیات بیتی محاسبه می شود:
x = ( ( x | 0b10101010 ) + x ) & 0b01010101 ( x = ( x & 0b01010101 ) - x ) & 0b01010101 if i> = j از این ویژگی می توان برای متعادل کردن مقدار Z استفاده کرد، برای مثال در دو بعد مختصات رو به بالا ( کاهش y ) ، پایین ( افزایش y ) ، سمت چپ ( کاهش x ) و سمت راست ( افزایش x ) از مقدار Z فعلی برابر است با:
( top = ( ( z & 0b10101010 ) - 1 & 0b10101010 ) | ( z & 0b01010101 ( bottom = ( ( z | 0b01010101 ) + 1 & 0b10101010 ) | ( z & 0b01010101 ( left = ( ( z & 0b01010101 ) - 1 & 0b01010101 ) | ( z & 0b10101010 ( right = ( ( z | 0b10101010 ) + 1 & 0b01010101 ) | ( z & 0b10101010 و به طور کلی برای اضافه کردن دو مقدار Z دو بعدی:
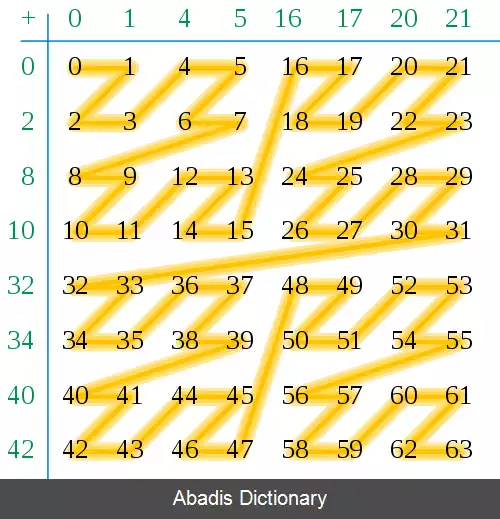
( sum = ( ( z | 0b10101010 ) + ( w & 0b01010101 ) & 0b01010101 ) | ( ( z | 0b01010101 ) + ( w & 0b10101010 ) & 0b10101010 ساختن چهاردرخت به طور مؤثر از مرتب سازی Z می توان برای ساختن یک چاردرخت برای مجموعه ای از نقاط استفاده کرد. [ ۳] ایدهٔ اصلی این است که مجموعهٔ ورودی را مطابق مرتبه Z مرتب کنید. پس از مرتب سازی، نقاط هم می توانند در یک درخت دودویی جستجوی ذخیره شوند و به طور مستقیم استفاده شوند، که به آن چاردرخت خطی گفته می شود، [ ۴] و هم می توانند برای ساخت یک چاردرخت مبتنی بر پوینتر استفاده شوند.

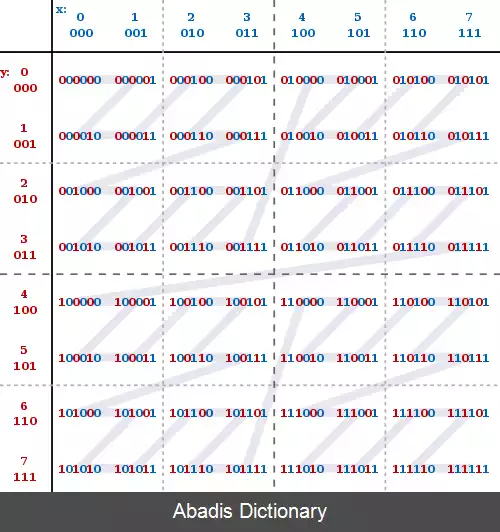
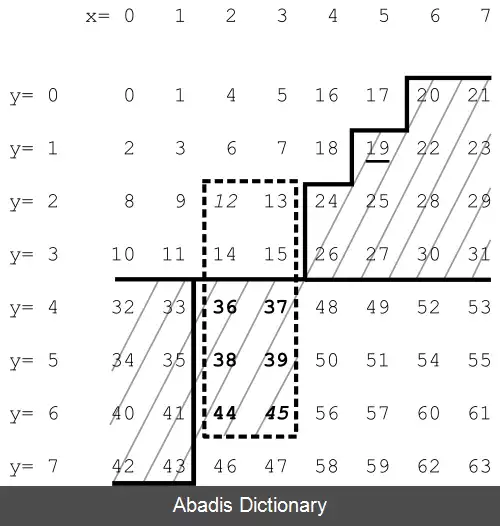
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفجدول زیر مقادیر Z را در دو بعد نشان می دهد که ۰ ≤ x ≤ ۷، ۰ ≤ y ≤ ۷ است ( هم در مبنای ۱۰ و هم به صورت دودویی نشان داده می شود ) در هم آمیختن مقادیر مختصات باینری مقادیر باینری z را بازمی گرداند. متصل کردن مقادیر z به ترتیب عددی آن ها یک خم بازگشتی Z شکل را می سازد.
مقادیر Z از xها به عنوان اعداد باینری از دنبالهٔ Moser–de Bruijn در نظر گرفته می شوند و فقط در موقعیت های مساوی خود دارای بیت های غیرصفر هستند:
{x = {0b000000, 0b000001, 0b000100, 0b000101, 0b010000, 0b010001, 0b010100, 0b010101 مجموع و تفاوت دو x با استفاده از عملیات بیتی محاسبه می شود:
x = ( ( x | 0b10101010 ) + x ) & 0b01010101 ( x = ( x & 0b01010101 ) - x ) & 0b01010101 if i> = j از این ویژگی می توان برای متعادل کردن مقدار Z استفاده کرد، برای مثال در دو بعد مختصات رو به بالا ( کاهش y ) ، پایین ( افزایش y ) ، سمت چپ ( کاهش x ) و سمت راست ( افزایش x ) از مقدار Z فعلی برابر است با:
( top = ( ( z & 0b10101010 ) - 1 & 0b10101010 ) | ( z & 0b01010101 ( bottom = ( ( z | 0b01010101 ) + 1 & 0b10101010 ) | ( z & 0b01010101 ( left = ( ( z & 0b01010101 ) - 1 & 0b01010101 ) | ( z & 0b10101010 ( right = ( ( z | 0b10101010 ) + 1 & 0b01010101 ) | ( z & 0b10101010 و به طور کلی برای اضافه کردن دو مقدار Z دو بعدی:
( sum = ( ( z | 0b10101010 ) + ( w & 0b01010101 ) & 0b01010101 ) | ( ( z | 0b01010101 ) + ( w & 0b10101010 ) & 0b10101010 ساختن چهاردرخت به طور مؤثر از مرتب سازی Z می توان برای ساختن یک چاردرخت برای مجموعه ای از نقاط استفاده کرد. [ ۳] ایدهٔ اصلی این است که مجموعهٔ ورودی را مطابق مرتبه Z مرتب کنید. پس از مرتب سازی، نقاط هم می توانند در یک درخت دودویی جستجوی ذخیره شوند و به طور مستقیم استفاده شوند، که به آن چاردرخت خطی گفته می شود، [ ۴] و هم می توانند برای ساخت یک چاردرخت مبتنی بر پوینتر استفاده شوند.






wiki: خم مرتبه زد
