در نظریه حلقه ها، ایده آل های نیم - اول ( به انگلیسی: Semiprime Ideals ) و حلقه های نیم - اول ( به انگلیسی: Semiprime Rings ) تعمیم ایده آل های اول اند. در جبر جابجایی، به ایده آل های نیم - اول، ایده آل های رادیکال هم می گویند.
به عنوان مثال، در حلقه اعداد صحیح، ایده آل های نیم - اول، ایده آل صفر و تمام ایده آل هایی به شکل n Z اند که در آن n یک عدد صحیح مربع - آزاد است. بنابر این، 30 Z یک ایده آل نیم - اول از اعداد صحیح است ( چون 30 = 2 × 3 × 5 و در تجزیه آن هیچ عامل اول تکراری مشاهده نمی شود ) ، اما 12 Z نیم - اول نیست ( چون 12 = 2 2 × 3 ، و تجزیه آن دارای عامل اول تکراری است ) .
دسته حلقه های نیم - اول شامل حلقه های نیم - ابتدایی، حلقه های اول و حلقه های تحویل یافته است.
بسیاری از تعاریف و گزاره های این مقاله در ( Lam 1999 ) و ( Lam 2001 ) ظاهر شده اند.
برای یک حلقه جابجایی چون R ، ایده آل محضی چون A را یک ایده آل نیم - اول گویند اگر A در هرکدام از دو تعریف معادل زیر صدق کند:
• اگر از x {\displaystyle x} در R {\displaystyle R} و برای عدد صحیح مثبتی چون k {\displaystyle k} از x k {\displaystyle x^{k}} در A {\displaystyle A} نتیجه شود که x {\displaystyle x} هم در A {\displaystyle A} باشد.
• اگر y {\displaystyle y} در R {\displaystyle R} باشد اما در A {\displaystyle A} نباشد، آنگاه تمام توان های صحیح مثبت y {\displaystyle y} هم در A {\displaystyle A} نباشند.
شرط دوم می گوید که متمم یک ایده آل نیم - اول "تحت توان گیری بسته است". این شرط مشابه خاصیت ایده آل های اول است که متممشان تحت ضرب بسته است.
همچون ایده آل های اول، خاصیت اخیر برای ایده آل های نیم - اول با کمک ایده آل ها به حلقه های ناجابجایی تعمیم پیدا می کند. شرایط زیر برای ایده آل نیم - اول A در یک حلقه R با هم معادلند:
• برای هر ایده آل J {\displaystyle J} از R {\displaystyle R} ، اگر برای هر عدد طبیعی k {\displaystyle k} داشته باشیم J k ⊆ A {\displaystyle J^{k}\subseteq A} آنگاه J ⊆ A {\displaystyle J\subseteq A} .
• برای هر ایده آل راست چون J {\displaystyle J} از R {\displaystyle R} ، اگر برای هر عدد طبیعی k {\displaystyle k} داشته باشیم J k ⊆ A {\displaystyle J^{k}\subseteq A} آنگاه J ⊆ A {\displaystyle J\subseteq A} .
• برای هر ایده آل چپ چون J {\displaystyle J} از R {\displaystyle R} ، اگر برای هر عدد طبیعی k {\displaystyle k} داشته باشیم J k ⊆ A {\displaystyle J^{k}\subseteq A} آنگاه J ⊆ A {\displaystyle J\subseteq A} .
• برای هر x {\displaystyle x} در R {\displaystyle R} ، اگر x R x ⊆ A {\displaystyle xRx\subseteq A} ، آنگاه x {\displaystyle x} در A {\displaystyle A} خواهد بود.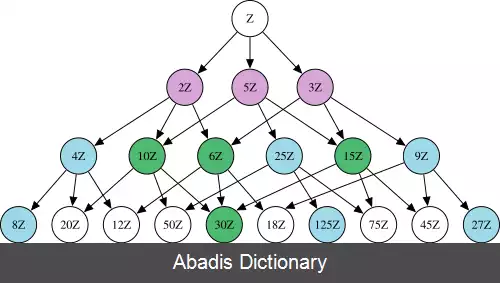
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه عنوان مثال، در حلقه اعداد صحیح، ایده آل های نیم - اول، ایده آل صفر و تمام ایده آل هایی به شکل n Z اند که در آن n یک عدد صحیح مربع - آزاد است. بنابر این، 30 Z یک ایده آل نیم - اول از اعداد صحیح است ( چون 30 = 2 × 3 × 5 و در تجزیه آن هیچ عامل اول تکراری مشاهده نمی شود ) ، اما 12 Z نیم - اول نیست ( چون 12 = 2 2 × 3 ، و تجزیه آن دارای عامل اول تکراری است ) .
دسته حلقه های نیم - اول شامل حلقه های نیم - ابتدایی، حلقه های اول و حلقه های تحویل یافته است.
بسیاری از تعاریف و گزاره های این مقاله در ( Lam 1999 ) و ( Lam 2001 ) ظاهر شده اند.
برای یک حلقه جابجایی چون R ، ایده آل محضی چون A را یک ایده آل نیم - اول گویند اگر A در هرکدام از دو تعریف معادل زیر صدق کند:
• اگر از x {\displaystyle x} در R {\displaystyle R} و برای عدد صحیح مثبتی چون k {\displaystyle k} از x k {\displaystyle x^{k}} در A {\displaystyle A} نتیجه شود که x {\displaystyle x} هم در A {\displaystyle A} باشد.
• اگر y {\displaystyle y} در R {\displaystyle R} باشد اما در A {\displaystyle A} نباشد، آنگاه تمام توان های صحیح مثبت y {\displaystyle y} هم در A {\displaystyle A} نباشند.
شرط دوم می گوید که متمم یک ایده آل نیم - اول "تحت توان گیری بسته است". این شرط مشابه خاصیت ایده آل های اول است که متممشان تحت ضرب بسته است.
همچون ایده آل های اول، خاصیت اخیر برای ایده آل های نیم - اول با کمک ایده آل ها به حلقه های ناجابجایی تعمیم پیدا می کند. شرایط زیر برای ایده آل نیم - اول A در یک حلقه R با هم معادلند:
• برای هر ایده آل J {\displaystyle J} از R {\displaystyle R} ، اگر برای هر عدد طبیعی k {\displaystyle k} داشته باشیم J k ⊆ A {\displaystyle J^{k}\subseteq A} آنگاه J ⊆ A {\displaystyle J\subseteq A} .
• برای هر ایده آل راست چون J {\displaystyle J} از R {\displaystyle R} ، اگر برای هر عدد طبیعی k {\displaystyle k} داشته باشیم J k ⊆ A {\displaystyle J^{k}\subseteq A} آنگاه J ⊆ A {\displaystyle J\subseteq A} .
• برای هر ایده آل چپ چون J {\displaystyle J} از R {\displaystyle R} ، اگر برای هر عدد طبیعی k {\displaystyle k} داشته باشیم J k ⊆ A {\displaystyle J^{k}\subseteq A} آنگاه J ⊆ A {\displaystyle J\subseteq A} .
• برای هر x {\displaystyle x} در R {\displaystyle R} ، اگر x R x ⊆ A {\displaystyle xRx\subseteq A} ، آنگاه x {\displaystyle x} در A {\displaystyle A} خواهد بود.

wiki: حلقه نیم اول
