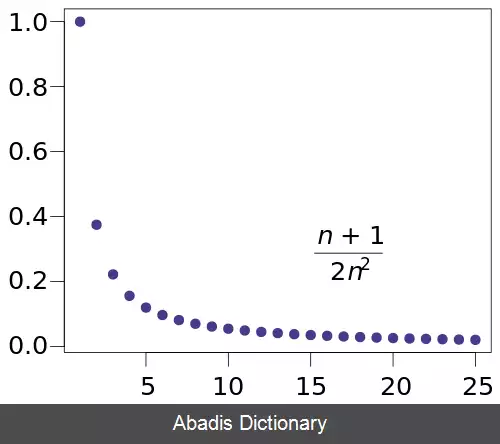
در حسابان، حد یک دنباله مقداری است که در صورت وجود، جمله های آن دنباله با پیش روی، به قدر دلخواه به آن نزدیک می شوند؛ اگر چنین مقداری وجود داشته باشد، دنباله را همگرا و در غیر این صورت دنباله را واگرا می نامیم. [ ۱]
به حد یک دنباله در بی نهایت «حد دنباله» می گویند.
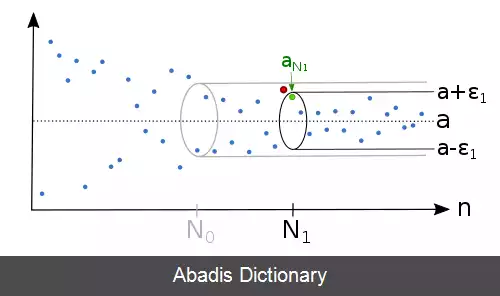
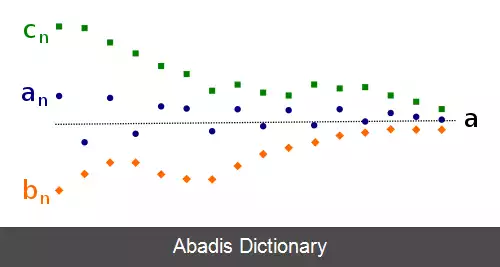
در نمایش مختصاتی، بازهٔ دوبعدی افقی حول مقدار y = A در نظر بگیرید ( به شکل مستطیلی افقی که به سمت راست تا بی نهایت ادامه دارد ) ، اگر دنبالهٔ { a n } n = 1 ∞ به A میل کند، باید از یک اندیس مشخّص ( N ) به بعد، همهٔ a n ها در این بازه باشند. این گزاره باید برای تمام بازه ها ( هر چند نازک ) ( به عرض 2 ε ) صدق کند.
به بیان دقیق تر، برای دنبالهٔ { a n } n = 1 ∞ [ ۲] :
lim n → ∞ a n = A ⟸ ∀ ε > 0 : ∃ N ∈ N : d ( a n , A ) < ε , ∀ n ≥ N
که ε مقدار نازک بودن بازه را نشان می دهد و d ( x , y ) در فضای متریک به معنای فاصلهٔ y و x است و به صورت | x − y | تعریف می شود.
در این صورت می نویسیم: lim n → ∞ a n = A
برای بعضی دنباله های واگرا نیز عبارتی همچون lim n → ∞ b n = ∞ یا lim n → ∞ b n = − ∞ نوشته می شود، یعنی ( به ترتیب ) دنبالهٔ { b n } n = 1 ∞ به بی نهایت یا منفی بی نهایت میل می کند؛ به عبارتی دیگر، ( به ترتیب ) دنبالهٔ { b n } n = 1 ∞ از بالا یا از پایین کران ندارد. به بیان دقیق:
lim n → ∞ b n = ∞ ⟸ ∀ B ∈ N : ∃ N ∈ N : b n > B , ∀ n ≥ N
دنبالهٔ واگرای a n = ( − 1 ) n از جمله مثال هایی ست که به هیچ مقداری میل نمی کند.
ویژگی های حد دنباله مثل ویژگی های حد تابع هستند.
حد دنباله در صورت وجود، یکتاست. یعنی اگر lim n → ∞ a n = A 1 و lim n → ∞ a n = A 2 آنگاه A 1 = A 2 [ ۲]
اگر برای دنبالهٔ { a n } n = 1 ∞ داشته باشیم lim n → ∞ a n = A ، به ازای هر تابع پیوسته ٔ f داریم lim n → ∞ f ( a n ) = lim n → ∞ f ( A )
lim n → ∞ ( a n ± b n ) = lim n → ∞ a n ± lim n → ∞ b n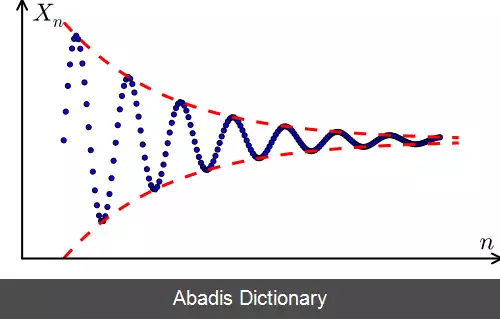

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه حد یک دنباله در بی نهایت «حد دنباله» می گویند.
در نمایش مختصاتی، بازهٔ دوبعدی افقی حول مقدار y = A در نظر بگیرید ( به شکل مستطیلی افقی که به سمت راست تا بی نهایت ادامه دارد ) ، اگر دنبالهٔ { a n } n = 1 ∞ به A میل کند، باید از یک اندیس مشخّص ( N ) به بعد، همهٔ a n ها در این بازه باشند. این گزاره باید برای تمام بازه ها ( هر چند نازک ) ( به عرض 2 ε ) صدق کند.
به بیان دقیق تر، برای دنبالهٔ { a n } n = 1 ∞ [ ۲] :
lim n → ∞ a n = A ⟸ ∀ ε > 0 : ∃ N ∈ N : d ( a n , A ) < ε , ∀ n ≥ N
که ε مقدار نازک بودن بازه را نشان می دهد و d ( x , y ) در فضای متریک به معنای فاصلهٔ y و x است و به صورت | x − y | تعریف می شود.
در این صورت می نویسیم: lim n → ∞ a n = A
برای بعضی دنباله های واگرا نیز عبارتی همچون lim n → ∞ b n = ∞ یا lim n → ∞ b n = − ∞ نوشته می شود، یعنی ( به ترتیب ) دنبالهٔ { b n } n = 1 ∞ به بی نهایت یا منفی بی نهایت میل می کند؛ به عبارتی دیگر، ( به ترتیب ) دنبالهٔ { b n } n = 1 ∞ از بالا یا از پایین کران ندارد. به بیان دقیق:
lim n → ∞ b n = ∞ ⟸ ∀ B ∈ N : ∃ N ∈ N : b n > B , ∀ n ≥ N
دنبالهٔ واگرای a n = ( − 1 ) n از جمله مثال هایی ست که به هیچ مقداری میل نمی کند.
ویژگی های حد دنباله مثل ویژگی های حد تابع هستند.
حد دنباله در صورت وجود، یکتاست. یعنی اگر lim n → ∞ a n = A 1 و lim n → ∞ a n = A 2 آنگاه A 1 = A 2 [ ۲]
اگر برای دنبالهٔ { a n } n = 1 ∞ داشته باشیم lim n → ∞ a n = A ، به ازای هر تابع پیوسته ٔ f داریم lim n → ∞ f ( a n ) = lim n → ∞ f ( A )
lim n → ∞ ( a n ± b n ) = lim n → ∞ a n ± lim n → ∞ b n





wiki: حد دنباله
