جستجوی بازه ای

جستجوی بازه ای در ساختمان داده ها، شامل پیش پردازش مجموعهٔ S از اشیا است تا مشخص شود کدام یک از اشیای S با بازهٔ مدنظر که شیء سؤال نیز نامیده می شود، تقاطع دارند. به عنوان مثال، اگر S، مجموعه ای از نقاط باشد که هریک متناظر با مختصات یک شهر است، یک نوع مسئلهٔ هندسی مورد نظر، یافتن شهرهایی که در محدودهٔ طول و عرض جغرافیایی داده شده واقع اند، می باشد.
مسئلهٔ جستجوی بازه ای و داده ساختارهایی که آن را حل می کنند، مسئله ای اساسی در هندسه محاسباتی است. این مسئله در حوزه هایی مانند سیستم های اطلاعات جغرافیایی ( GIS ) ، طراحی به کمک کامپیوتر ( CAD ) و پایگاه داده ها کاربرد دارد.
صورت های گوناگونی از این مسئله وجود دارد که به تبع آن داده ساختارهای گوناگونی مورد استفاده قرار داده می گیرند. [ ۱] برای داشتن راه حل بهینه، موارد مختلفی باید مدنظر قرار داده شوند از جمله:
• نوع اشیای مورد جستجو: الگوریتم ها بر اساس نوع اشیای مورد بررسی انتخاب می شوند، برای مثال می توان نقاط، خطوط، چندضلعی ها را مورد بررسی قرار داد. ساده ترین اشیا نیز نقاط هستند که بیشتر از سایر اشیاء مورد بررسی قرار گرفته اند.
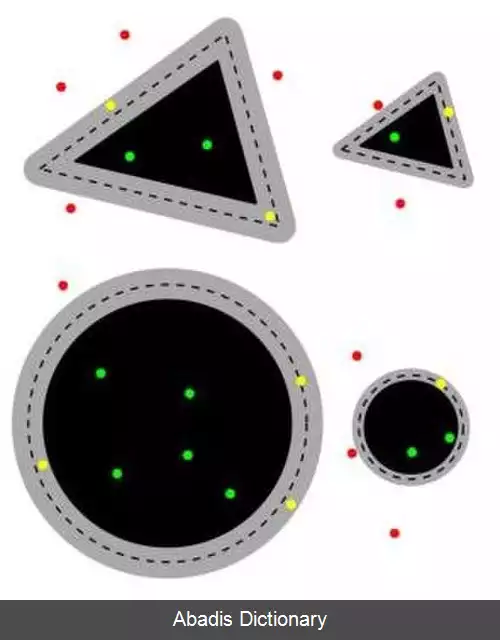
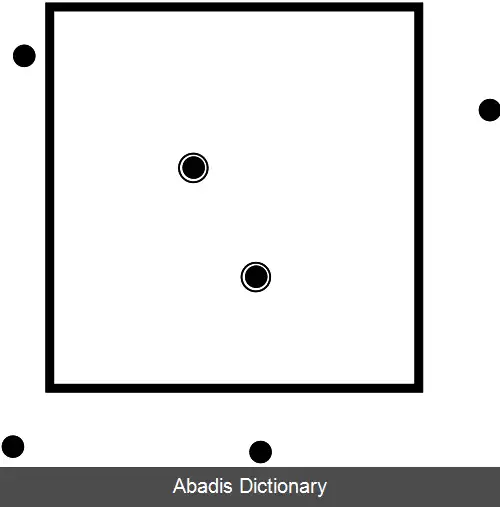
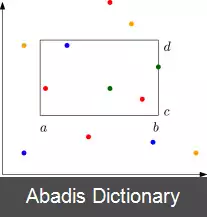
• نوع بازه: بازهٔ مورد بررسی باید برای یک مجموعهٔ از پیش تعیین شده مشخص گردد. بازه هایی که تاکنون بیشتر مورد بررسی قرار گرفته اند و مسائل حل شده با آن ها مستطیل های محوری ( جستجوی بازه ای قائم ) ، کره ها و دایرهها، نیم فاصلهله ها هستند.
• سؤال مطرح شده: اگر بخواهیم لیست اشیایی را که مجدودهٔ سوالات را تقسیم می کنند گزارش کنیم، آنگاه مسئله تبدیل به یک گزارش بازه ای خواهد شد. اگر بخواهیم تنها تعداد اشیایی که با بازه تقاطع دارند را بررسی کنیم، آنگاه با مسئلهٔ شمارش بازه ای مواجه ایم.
• تفاوت جستجوی بازه ای پویا با جستجوی بازه ای ایستا: در حالت ایستا، مجموعهٔ S، از ابتدا مشخص است و تا پایان تغییری نمی کند. در حالت پویا، اشیای جدیدی اضافه یا اشیای قبلی حذف می شوند.
• مفهوم جستجوی بازه ای آفلاین: هم مجموعهٔ اشیا و هم مجموعهٔ سوالات از ابتدا مشخص هستند.
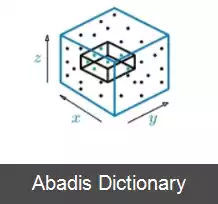
در جستجوی بازه ای قائم، مجموعهٔ S از n نقطه و d بُعد تشکیل شده است و مجموعهٔ مورد پرسش، بازه هایی در این ابعاد است؛ بنابراین مجموعهٔ مورد پرسش از مستطیل های محوری چندبعدی تشکیل شده است. اگر اندازهٔ خروجی را k در نظر بگیریم، جان بنتلی با استفاده از یک درخت کی دی توانست در زمان O ( n 1 − 1 d + k ) ( پیچیدگی زمانی ) و با حافظهٔ O ( n ) این مسئله را حل کند. [ ۲] همچنین بنتلی با استفاده از داده ساختار درخت بازه ای، توانست زمان مورد نیاز برای حل این مسئله را به O ( log d ⁡ n + k ) برساند. البته در این حالت حافظهٔ مورد نیاز به O ( n log d − 1 ⁡ n ) افزایش پیدا کرد. [ ۳] دن ویلارد نیز با استفاده از داده ساختار دیگری توانست این مسئله را در زمان O ( log d − 1 ⁡ n + k ) حل کند.