جدول کارنو ( به انگلیسی: Karnaugh map ) ( اختصاری KM یا K - map ) روشی است برای ساده سازی توابع جبر بولی که به وسیلهٔ موریس کارنو در سال ۱۹۵۳ ارائه شد. این روش کامل شده دیاگرام ویچ است که در سال ۱۹۵۲ توسط ادوارد ویچ ارائه شده بود. جدول کارنو نیاز به محاسبات طولانی را کاهش داده و به مشخص کردن و حذف کردن سریع وضعیت رقابتی کمک می کند.
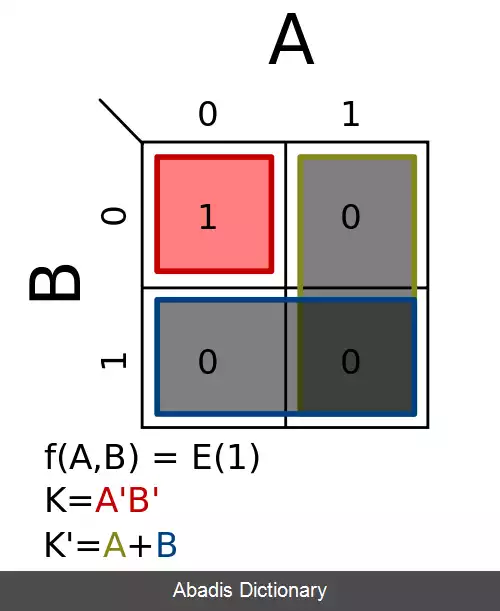
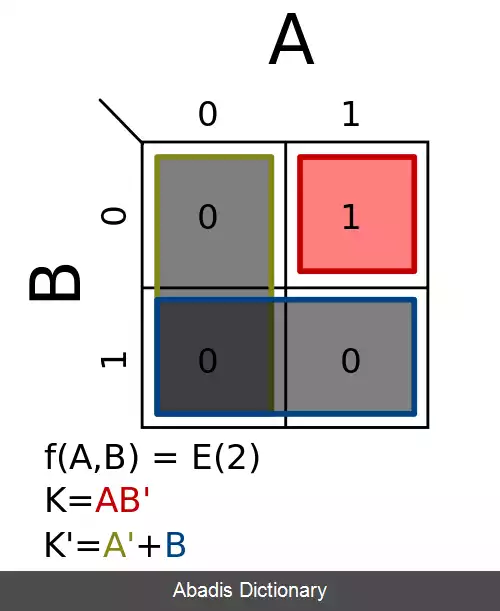
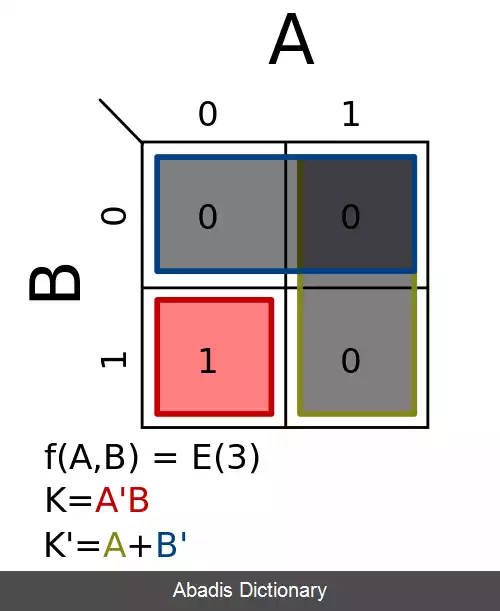
مقادیر بولی از جدول ارزش و با توجه به اصول کد گری به جدول کارنو انتقال می یابند. داده ها در جدول کارنو که ۲n سلول دارد چیده می شوند و مینترم ها بر اساس اصول جبر بول ساخته می شوند.
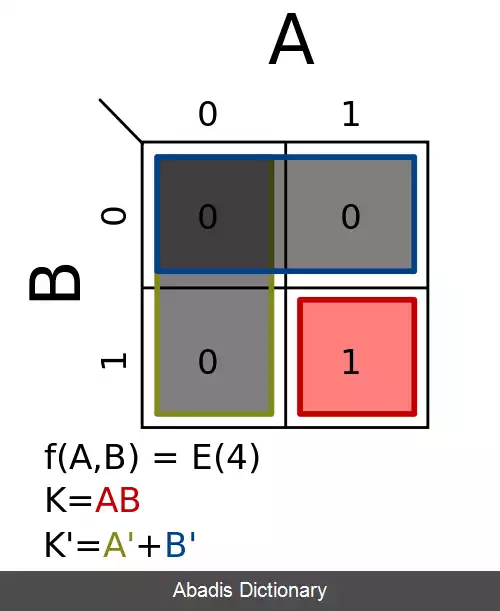
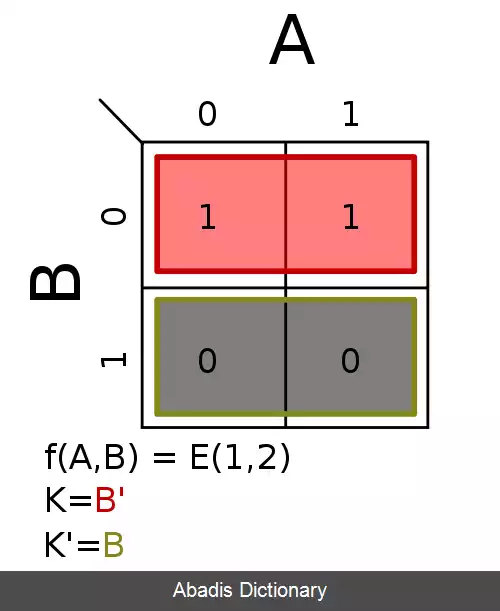
جدول کارنو نموداری از مربع ها است که هر مربع یک مینترم را نمایش میدهد. به کمک این مربع ها می توان یک تابع بول را نمایش داد. جدول کارنو به چند حالت مختلف دو، سه، چهار و گاهی پنج متغیره نمایش می یابد. جدول کارنوی n متغیره، دارای 2n خانه است که هر خانه یک مینترم را نمایش می دهد. بعد از اینکه مینترم های یک تابع را در جدول کارنو علامت گذاری کردیم، می توانیم مربع های همجوار را با هم ساده کنیم. در شکل زیر یک نقشه ۴ متغیره که ۱۶ مربع یا خانه دارد نمایش داده شده است:
برای شماره گذاری خانه ها از کد گری استفاده شده است. چرا که در کد گری، هر عدد با اعداد ماقبل و مابعد خود تنها در یک رقم تفاوت دارد و این خاصیت به ساده کردن توابع بول کمک می کند.
مثال زیر یک تابع ساده نشده جبر بول را با متغیرهای بولی A, B، C, D نشان می دهد.
f ( A , B , C , D ) = ∑ ( 5 , 6 , 8 , 9 )
جدول صحت تابع به صورت زیر ساخته می شود:
تابع فوق با دو نماد گذاری در زیر نمایش داده شده است. در اولی m i ها مینترم نامیده می شوند که شماره سطرهایی که در جدول درستی مقدار یک دارند را نمایش می دهند و در نماد گذاری دوم M i ها ماکسترم هستند و نمایانگر شماره سطرهایی که در جدول درستی مقدار صفر دارند هستند.
• f ( A , B , C , D ) = ∑ m i , i ∈ { 6 , 8 , 9 , 10 , 11 , 12 , 13 , 14 } {\displaystyle f ( A, B, C, D ) =\sum _{}m_{i}, i\in \{6, 8, 9, 10, 11, 12, 13, 14\}}
• f ( A , B , C , D ) = ∏ M i , i ∈ { 0 , 1 , 2 , 3 , 4 , 5 , 7 , 15 } {\displaystyle f ( A, B, C, D ) =\prod _{}M_{i}, i\in \{0, 1, 2, 3, 4, 5, 7, 15\}}
در مثال بالا، برای جدول کارنو چهار متغیره ۱۶ حالت وجود دارد و در نتیجه جدول درستی آن ۱۶ سطر دارد. جدول کارنو در یک صفحه مشبک ۴*۴ تنظیم می شود.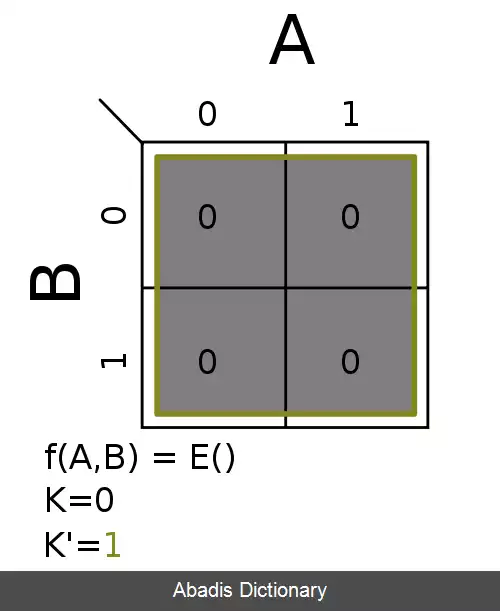
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمقادیر بولی از جدول ارزش و با توجه به اصول کد گری به جدول کارنو انتقال می یابند. داده ها در جدول کارنو که ۲n سلول دارد چیده می شوند و مینترم ها بر اساس اصول جبر بول ساخته می شوند.
جدول کارنو نموداری از مربع ها است که هر مربع یک مینترم را نمایش میدهد. به کمک این مربع ها می توان یک تابع بول را نمایش داد. جدول کارنو به چند حالت مختلف دو، سه، چهار و گاهی پنج متغیره نمایش می یابد. جدول کارنوی n متغیره، دارای 2n خانه است که هر خانه یک مینترم را نمایش می دهد. بعد از اینکه مینترم های یک تابع را در جدول کارنو علامت گذاری کردیم، می توانیم مربع های همجوار را با هم ساده کنیم. در شکل زیر یک نقشه ۴ متغیره که ۱۶ مربع یا خانه دارد نمایش داده شده است:
برای شماره گذاری خانه ها از کد گری استفاده شده است. چرا که در کد گری، هر عدد با اعداد ماقبل و مابعد خود تنها در یک رقم تفاوت دارد و این خاصیت به ساده کردن توابع بول کمک می کند.
مثال زیر یک تابع ساده نشده جبر بول را با متغیرهای بولی A, B، C, D نشان می دهد.
f ( A , B , C , D ) = ∑ ( 5 , 6 , 8 , 9 )
جدول صحت تابع به صورت زیر ساخته می شود:
تابع فوق با دو نماد گذاری در زیر نمایش داده شده است. در اولی m i ها مینترم نامیده می شوند که شماره سطرهایی که در جدول درستی مقدار یک دارند را نمایش می دهند و در نماد گذاری دوم M i ها ماکسترم هستند و نمایانگر شماره سطرهایی که در جدول درستی مقدار صفر دارند هستند.
• f ( A , B , C , D ) = ∑ m i , i ∈ { 6 , 8 , 9 , 10 , 11 , 12 , 13 , 14 } {\displaystyle f ( A, B, C, D ) =\sum _{}m_{i}, i\in \{6, 8, 9, 10, 11, 12, 13, 14\}}
• f ( A , B , C , D ) = ∏ M i , i ∈ { 0 , 1 , 2 , 3 , 4 , 5 , 7 , 15 } {\displaystyle f ( A, B, C, D ) =\prod _{}M_{i}, i\in \{0, 1, 2, 3, 4, 5, 7, 15\}}
در مثال بالا، برای جدول کارنو چهار متغیره ۱۶ حالت وجود دارد و در نتیجه جدول درستی آن ۱۶ سطر دارد. جدول کارنو در یک صفحه مشبک ۴*۴ تنظیم می شود.






wiki: جدول کارنو
