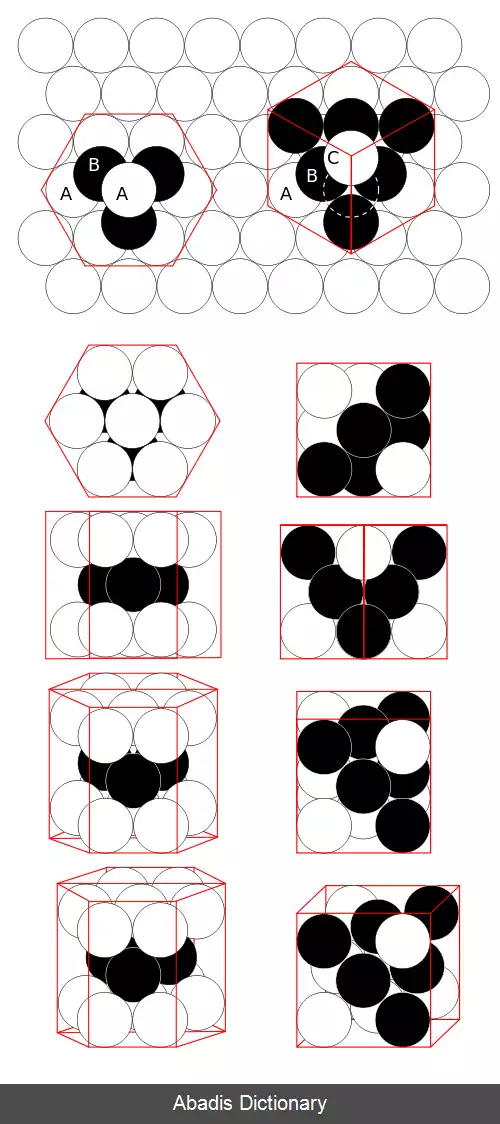
در هندسه، مفهوم جاسازی گوی ها ( به انگلیسی: sphere packing ) به نوعی از چیدمان کره های ناهمپوشان در یک فضای مشخص اشاره دارد. گوی های در نظر گرفته شده معمولاً همگی اندازه یکسان دارند و فضا معمولاً فضای اقلیدسی سه بعدی است. با این حال، مشکلات جاسازی کُره ها را می توان به موارد گوی های نابرابر، فضاهایی با ابعاد دیگر ( که در آن مشکل تبدیل به جاسازی دایره ای در دو بعد یا جاسازی اَبَرکره در ابعاد بالاتر می شود ) یا به فضاهای نااقلیدسی مانند فضای هذلولی تعمیم داد.
یک مشکل ویژه برای جاسازی گوی ها، یافتن آرایشی است که در آن گوی ها تا حد امکان فضا را پر کنند. نسبت فضای پرشده توسط کره ها را چگالی جاسازی می گویند. از آنجایی که چگالی محلی یک جاسازی در یک فضای نامتناهی می تواند بسته به حجمی که روی آن اندازه گیری می شود متفاوت باشد، مشکل معمولاً به حداکثر رساندن چگالی متوسط یا مجانبی است که در یک حجم به اندازه کافی بزرگ اندازه گیری می شود.
برای کره های مساوی در حالت سه بعدی، متراکم ترین جاسازی تقریباً ۷۴ درصد حجم را مصرف می کند. یک جاسازی تصادفی از گوی های هم اندازه معمولاً دارای چگالی حدود ۶۳٫۵٪ است. [ ۱]
آرایش مشبکه ( که معمولاً آرایش منظم نامیده می شود ) آرایشی است که در آن مراکز کره ها یک الگوی بسیار متقارن را تشکیل می دهند که فقط به n بردار نیاز دارد تا به طور یکتا تعریف شوند ( در فضای اقلیدسی n بعدی ) . ترتیبات مشبکه دوره ای هستند. آرایش هایی که در آن گوی ها یک شبکه تشکیل نمی دهند ( اغلب نامنظم نامیده می شوند ) همچنان می توانند دوره ای باشند، اما همچنین نامنظم ( به عبارت درست غیر تناوبی ) یا تصادفی باشند. به دلیل تقارن بالایی که دارند، دسته بندی جاسازی های مشبک نسبت به غیر مشبک آسان تر است. شبکه های تناوبی همیشه چگالی مشخصی دارند.


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک مشکل ویژه برای جاسازی گوی ها، یافتن آرایشی است که در آن گوی ها تا حد امکان فضا را پر کنند. نسبت فضای پرشده توسط کره ها را چگالی جاسازی می گویند. از آنجایی که چگالی محلی یک جاسازی در یک فضای نامتناهی می تواند بسته به حجمی که روی آن اندازه گیری می شود متفاوت باشد، مشکل معمولاً به حداکثر رساندن چگالی متوسط یا مجانبی است که در یک حجم به اندازه کافی بزرگ اندازه گیری می شود.
برای کره های مساوی در حالت سه بعدی، متراکم ترین جاسازی تقریباً ۷۴ درصد حجم را مصرف می کند. یک جاسازی تصادفی از گوی های هم اندازه معمولاً دارای چگالی حدود ۶۳٫۵٪ است. [ ۱]
آرایش مشبکه ( که معمولاً آرایش منظم نامیده می شود ) آرایشی است که در آن مراکز کره ها یک الگوی بسیار متقارن را تشکیل می دهند که فقط به n بردار نیاز دارد تا به طور یکتا تعریف شوند ( در فضای اقلیدسی n بعدی ) . ترتیبات مشبکه دوره ای هستند. آرایش هایی که در آن گوی ها یک شبکه تشکیل نمی دهند ( اغلب نامنظم نامیده می شوند ) همچنان می توانند دوره ای باشند، اما همچنین نامنظم ( به عبارت درست غیر تناوبی ) یا تصادفی باشند. به دلیل تقارن بالایی که دارند، دسته بندی جاسازی های مشبک نسبت به غیر مشبک آسان تر است. شبکه های تناوبی همیشه چگالی مشخصی دارند.




wiki: جاسازی گوی ها
