در آمار و احتمال توزیع پواسون ( به انگلیسی: Poisson distribution، /ˈpwɑːsɒn/ ) ( یا قانون پواسون اعداد کوچک ) یک توزیع احتمالی گسسته است که احتمال اینکه یک حادثه به تعداد مشخصی در فاصلهٔ زمانی یا مکانی ثابتی رخ دهد را شرح می دهد؛ به شرط اینکه این حوادث با نرخ میانگین مشخصی و مستقل از زمان آخرین حادثه رخ دهند. ( توزیع پواسون همچنین برای تعدادی از حوادث در فاصله های مشخص دیگری مثل مسافت، مساحت یا حجم استفاده شود ) این توزیع برای اولین بار توسط Siméon Denis Poisson 1781 - 1840 معرفی و به ضمیمه تئوری احتمال او در سال ۱۸۳۸ در یکی از کتاب هایش بنامRecherches sur la probabilité des jugements en matière criminelle et en matière civile ( جستاری در احتمال قضاوت ها در مسائل کیفری و حقوقی ) چاپ شد. اولین استفادهٔ عملی از این توزیع به سال ۱۸۹۸ برمی گردد جایی که Ladislaus Bortkiewicz به بررسی تعداد تصادفی از سربازان ارتش پروس که توسط پا زدن اسب کشته شدند می پردازد. این اثر بیشتر بر متغیرهای تصادفی خاصی تأکید می کند مانند متغیر تصادفی N که تعداد ظهورها ( یا ورودهای ) گسسته را که در فاصله زمانی مشخصی اتفاق می افتند را می شمارد. توزیع پواسن در هر زمینه ای استفاده می شود برای مثال: فرض کنید شخصی به طور متوسط چهار ایمیل در روز دریافت می کند تعداد ایمیل های دریافت شده در برخی از روزها می تواند کمی کمتر یا بیشتر از چهار باشد ولی در بازه زمانی طولانی اگر بر دریافت ایمیل نظارت کنیم، می بینیم نرخ دریافت ثابت است. حال فرض کنید فرایند یا ترکیبی از چند فرایند یک جریان رویداد به صورت تصادفی تولید کنند، توزیع پواسن احتمال اینکه تعداد این رخدادها ۲٬۳٬۴ و اعداد دیگر باشد را مشخص می کند. توزیع پواسن درجه پراکندگی اطراف نرخ متوسط وقوع رخداد را پیش بینی می کند.
• در سیستم های الکتریکی: تعداد دفعاتی که زنگ یک تلفن به صدا در می آید
• در نجوم: فوتون هایی که به تلسکوپ می رسند
• در صنعت: تعداد محصولات معیوب یک کارخانه
• در فیزیک: تعداد ذرات؛ alpha انتشار یافته در یک ثانیه
• در زیست شناسی: تعداد جهش ها روی یک رشتهٔ معین از DNA دارای توزیع پواسن است.
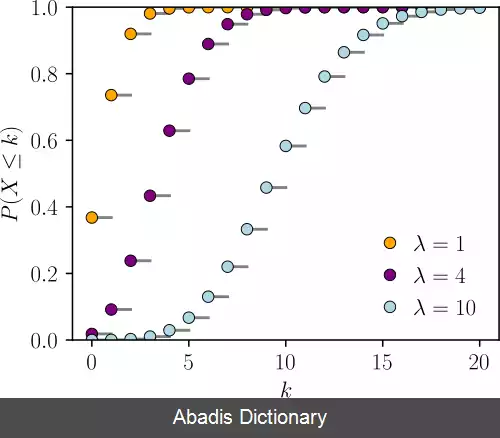
اگر امید ریاضی ظهورها در این بازه λ باشد، احتمال اینکه دقیقاً k ظهور داشته باشیم ( k عدد صحیح نامنفی است، k=۰، ۱، ۲، … ) برابر است با: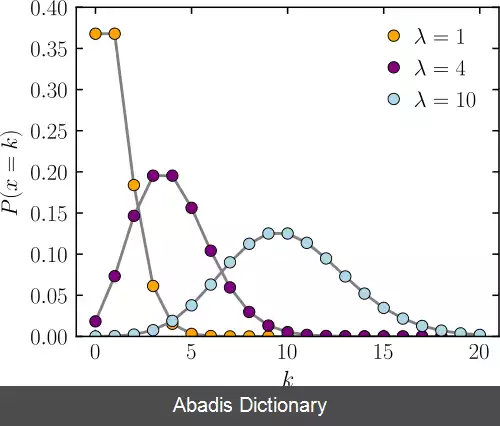
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• در سیستم های الکتریکی: تعداد دفعاتی که زنگ یک تلفن به صدا در می آید
• در نجوم: فوتون هایی که به تلسکوپ می رسند
• در صنعت: تعداد محصولات معیوب یک کارخانه
• در فیزیک: تعداد ذرات؛ alpha انتشار یافته در یک ثانیه
• در زیست شناسی: تعداد جهش ها روی یک رشتهٔ معین از DNA دارای توزیع پواسن است.
اگر امید ریاضی ظهورها در این بازه λ باشد، احتمال اینکه دقیقاً k ظهور داشته باشیم ( k عدد صحیح نامنفی است، k=۰، ۱، ۲، … ) برابر است با:


wiki: توزیع پواسون
