در نظریه احتمال و آمار، توزیع نرمال چند متغیره، توزیع گاوسی چند متغیره، یا توزیع نرمال توأم یک تعمیم از توزیع نرمال یک بعدی ( تک متغیره ) به ابعاد بالاتر است. یک تعریف این است که اگر هر ترکیب خطی از k عضو یک بردار، توزیع نرمال تک متغیره داشته باشد، به یک بردار تصادفی k متغیره گفته می شود که به طور نرمال توزیع شده است. اهمیت آن عمدتاً از قضیه حد مرکزی چند متغیره ناشی می شود. برای توصیف هر مجموعه ای از متغیرهای تصادفی با ارزش حقیقی که احتمالاً همبسته اند و هر کدام حول مقداری متوسط جمع می شوند، اغلب از توزیع نرمال چندمتغییره استفاده می شود.
توزیع نرمال چند متغیره یک بردار تصادفی k بعدی به صورت X = ( X 1 , … , X k ) T را می توان با نماد زیر نوشت:
یا برای اینکه با صراحت نشان دهیم X از بعد k است،
با بردار میانگین k بعدی
و ماتریس کوواریانس k × k
به طوری که 1 ≤ i , j ≤ k . معکوس ماتریس کوواریانس را ماتریس دقت می نامند که به صورت Q = Σ − 1 نمایش داده می شود.
یک بردار تصادفی حقیقی به صورت X = ( X 1 , … , X k ) T ، بردار تصادفی نرمال استاندارد نامیده می شود اگر تمام اعضای X n مستقل و هر کدام یک متغیر تصادفی با میانگین صفر و واریانس ۱ باشند که به طور نرمال توزیع شده اند یعنی X n ∼ N ( 0 , 1 ) برای همه n ها. : p. 454
یک بردار تصادفی حقیقی به صورت X = ( X 1 , … , X k ) T ، بردار تصادفی نرمال متمرکز نامیده می شود اگر ماترس A با ابعاد k × ℓ وجود داشته باشد به طوری که A Z توزیع مشابهی با X داشته و Z یک بردار تصادفی نرمال استاندار ℓ متغیره باشد. : p. 454
یک بردار تصادفی حقیقی به صورت X = ( X 1 , … , X k ) T ، بردار تصادفی معمولی نامیده می شود اگر بردار تصادفی نرمال استاندارد Z با بعد ℓ ، بردار μ با بعد k و ماتریس A با ابعاد k × ℓ وجود داشته باشد، به طوری که X = A Z + μ . : p. 454 : p. 455
به نمادگذاری ریاضی:
X ∼ N ( μ , Σ ) ⟺ there exist μ ∈ R k , A ∈ R k × ℓ such that X = A Z + μ for Z n ∼ N ( 0 , 1 ) , i. i. d.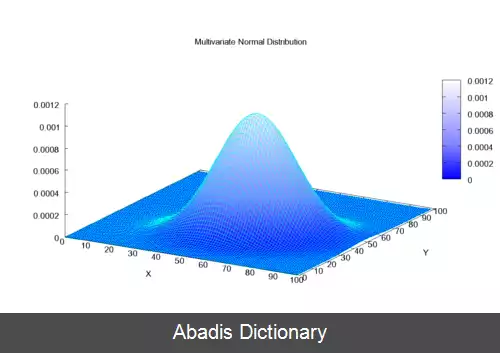
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتوزیع نرمال چند متغیره یک بردار تصادفی k بعدی به صورت X = ( X 1 , … , X k ) T را می توان با نماد زیر نوشت:
یا برای اینکه با صراحت نشان دهیم X از بعد k است،
با بردار میانگین k بعدی
و ماتریس کوواریانس k × k
به طوری که 1 ≤ i , j ≤ k . معکوس ماتریس کوواریانس را ماتریس دقت می نامند که به صورت Q = Σ − 1 نمایش داده می شود.
یک بردار تصادفی حقیقی به صورت X = ( X 1 , … , X k ) T ، بردار تصادفی نرمال استاندارد نامیده می شود اگر تمام اعضای X n مستقل و هر کدام یک متغیر تصادفی با میانگین صفر و واریانس ۱ باشند که به طور نرمال توزیع شده اند یعنی X n ∼ N ( 0 , 1 ) برای همه n ها. : p. 454
یک بردار تصادفی حقیقی به صورت X = ( X 1 , … , X k ) T ، بردار تصادفی نرمال متمرکز نامیده می شود اگر ماترس A با ابعاد k × ℓ وجود داشته باشد به طوری که A Z توزیع مشابهی با X داشته و Z یک بردار تصادفی نرمال استاندار ℓ متغیره باشد. : p. 454
یک بردار تصادفی حقیقی به صورت X = ( X 1 , … , X k ) T ، بردار تصادفی معمولی نامیده می شود اگر بردار تصادفی نرمال استاندارد Z با بعد ℓ ، بردار μ با بعد k و ماتریس A با ابعاد k × ℓ وجود داشته باشد، به طوری که X = A Z + μ . : p. 454 : p. 455
به نمادگذاری ریاضی:
X ∼ N ( μ , Σ ) ⟺ there exist μ ∈ R k , A ∈ R k × ℓ such that X = A Z + μ for Z n ∼ N ( 0 , 1 ) , i. i. d.



wiki: توزیع نرمال چند متغیره
