توزیع فوق هندسی
فرهنگستان زبان و ادب
دانشنامه عمومی
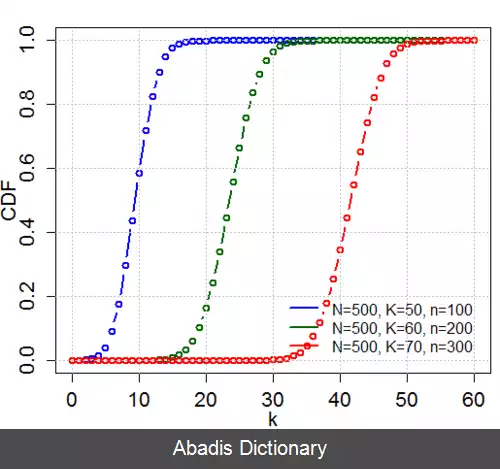
توزیع فوقِ هندسی[ ۱] ( به انگلیسی: Hypergeometric distribution ) مجموعه ای از N عضو را در نظر بگیرید که k عضو آن دارای یک ویژگی و بقیه، فاقد این ویژگی هستند. مانند 500 لامپ موجود در یک جعبه که 300 تای آن سالم و بقیه معیوب باشند. حال فرض کنید می خواهیم از این مجموعه، n عضو به صورت تصادفی ( بدون جایگذاری ) انتخاب کنیم. دراین صورت اگر متغیر تصادفی X تعداد عناصری در n برداشت باشد که دارای ویژگی موردنظر هستند، می گوئیم X دارای توزیع فوق هندسی است.
ابتدا برای درک بهتر این توزیع یک مثال مطرح می کنیم. فرض کنید از جعبه ای شامل D فیوز معیوب و N - D فیوز سالم، n فیوز را به طور تصادفی و بدون جایگذاری انتخاب کنیم. به علاوه فرض کنیدn، تعداد فیوزهای استخراجی از تعداد فیوزهای معیوب و فیوزهای سالم تجاوز نکند. فرض کنید متغیرتصادفی X تعداد فیوزهای معیوب خارج شده باشد. بنابراین: تعریف: فرض کنید D, N و n اعداد صحیح و مثبت اند، با n ≤ m i n ( D , N − D ) . دراینصورت،
p ( k ) = P ( X = k ) = ( D k ) ( N − D n − k ) ( N n ) f o r k ∈ 0 , 1 , 2 , . . . , n
را تابع جرم احتمال توزیع فوق هندسی می گویند.
با استفاده از اتحاد ترکیبیاتی واندرموند به راحتی می توان نتیجه گرفت که
که با استفاده از آن برای همه ی مقادیر k به سادگی می توان ∑ k = 0 n p ( k ) = 1 را نتیجه گرفت.
برای متغیرتصادفی فوق هندسی X که در بالا تعریف شد داریم:
توجه کنید که اگر آزمایش ستخراج n قلم کالا از جعبه ای شامل D قلم کالای معیوب و N - D قلم کالای سالم را با جایگذاری انجام دهیم، دراینصورت X دارای توزیع دوجمله ای با پارامترهای n و D N است. پس:
اینها نشان می دهند که اگر اقلام با جایگذاری انتخاب شوند، دراینصورت امیدریاضی X تغییر نمی کند اما واریانس X افزایش پیدامی کند. با وجود این اگر n بسیار کوچکتر از N باشد دراینصورت باتوجه به فرمول واریانس، استخراج باجایگذاری تقریب خوبی برای استخراج بدون جایگذاری است.
در یک کیسه 24 مهره وجود دارد که 4 تای آن قرمز و مابقی سفید هستند. اگر از این کیسه 6 مهره به تصادف و بدون جایگذاری برداریم وX تعداد مهره های قرمز باشد؛ توزیع احتمال X را به دست آورید. احتمال اینکه هیچ مهره قرمزی بدست نیاید چقدر است؟ داریم n=6 , D=4 , N=24 بنابراین توزیع احتمال X فوق هندسی و به صورت زیر است: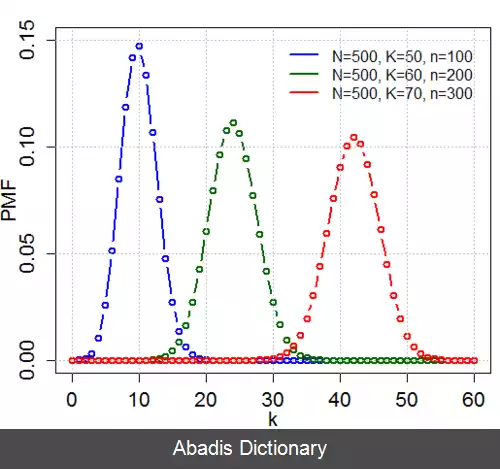
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفابتدا برای درک بهتر این توزیع یک مثال مطرح می کنیم. فرض کنید از جعبه ای شامل D فیوز معیوب و N - D فیوز سالم، n فیوز را به طور تصادفی و بدون جایگذاری انتخاب کنیم. به علاوه فرض کنیدn، تعداد فیوزهای استخراجی از تعداد فیوزهای معیوب و فیوزهای سالم تجاوز نکند. فرض کنید متغیرتصادفی X تعداد فیوزهای معیوب خارج شده باشد. بنابراین: تعریف: فرض کنید D, N و n اعداد صحیح و مثبت اند، با n ≤ m i n ( D , N − D ) . دراینصورت،
p ( k ) = P ( X = k ) = ( D k ) ( N − D n − k ) ( N n ) f o r k ∈ 0 , 1 , 2 , . . . , n
را تابع جرم احتمال توزیع فوق هندسی می گویند.
با استفاده از اتحاد ترکیبیاتی واندرموند به راحتی می توان نتیجه گرفت که
که با استفاده از آن برای همه ی مقادیر k به سادگی می توان ∑ k = 0 n p ( k ) = 1 را نتیجه گرفت.
برای متغیرتصادفی فوق هندسی X که در بالا تعریف شد داریم:
توجه کنید که اگر آزمایش ستخراج n قلم کالا از جعبه ای شامل D قلم کالای معیوب و N - D قلم کالای سالم را با جایگذاری انجام دهیم، دراینصورت X دارای توزیع دوجمله ای با پارامترهای n و D N است. پس:
اینها نشان می دهند که اگر اقلام با جایگذاری انتخاب شوند، دراینصورت امیدریاضی X تغییر نمی کند اما واریانس X افزایش پیدامی کند. با وجود این اگر n بسیار کوچکتر از N باشد دراینصورت باتوجه به فرمول واریانس، استخراج باجایگذاری تقریب خوبی برای استخراج بدون جایگذاری است.
در یک کیسه 24 مهره وجود دارد که 4 تای آن قرمز و مابقی سفید هستند. اگر از این کیسه 6 مهره به تصادف و بدون جایگذاری برداریم وX تعداد مهره های قرمز باشد؛ توزیع احتمال X را به دست آورید. احتمال اینکه هیچ مهره قرمزی بدست نیاید چقدر است؟ داریم n=6 , D=4 , N=24 بنابراین توزیع احتمال X فوق هندسی و به صورت زیر است:


wiki: توزیع فوق هندسی
پیشنهاد کاربران
" پخش فرا هندسی ":توزیع فوق هندسی.
