توزیع ریلی یا رایلی ( به انگلیسی: Rayleigh distribution ) معمولاً در مواردی مشاهده می شود که متغیری دارای دو عضو بوده که هر دو دارای توزیع نرمال با واریانس مشابه بوده و از هم مستقل باشند. به طور مثال می توان سرعت باد که دارای دو مؤلفه ( در جهت شرقی−غربی و شمالی−جنوبی ) می باشد را دارای این توزیع دانست. همچنین اندازه اعداد مختلطی که مقادیر حقیقی و موهومی آنها دارای توزیع یکسان نرمال بوده و از هم مستقل باشند، دارای توزیع ریلی است. این توزیع به نام لرد ریلی نامیده شده است.
تابع چگالی احتمال یک توزیع رایلی چنین است.
که در این رابطه σ پارامتر مقیاس توزیع نامیده می شود.
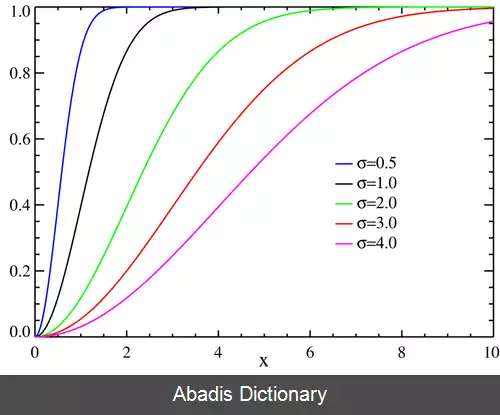
تابع توزیع تجمعی در توزیع رایلی برابر است با:
در حالی که . x ∈ [ 0 , ∞ )
میانه در توزیع رایلی برابر است با:
σ π 2
مد در توزیع رایلی برابر است با:
σ
میانگین یک توزیع رایلی برابر است با:
واریانس یک توزیع رایلی برابر است با:
4 − π 2 σ 2
توزیع رایلی معمولا برای مدل کردن ارتفاع موج ها در علوم اقیانوس شناسی استفاده می شود و همچنین برای بررسی بیشینه انرژی دریافتی از موج های رادیویی نیز استفاده می شود. در گذشته هم برای مدل سازی فرکانس سرعت باد در توربین های بادی در طول یک سال مورد استفاده واقع می شده است. [ ۱]
• R ∼ R a y l e i g h ( σ ) {\displaystyle R\sim \mathrm {Rayleigh} ( \sigma ) } اگر R = X 2 + Y 2 {\displaystyle R={\sqrt {X^{2}+Y^{2}}}} و X ∼ N ( 0 , σ 2 ) {\displaystyle X\sim N ( 0, \sigma ^{2} ) } و Y ∼ N ( 0 , σ 2 ) {\displaystyle Y\sim N ( 0, \sigma ^{2} ) } دو متغیر مستقل با توزیع نرمال باشند.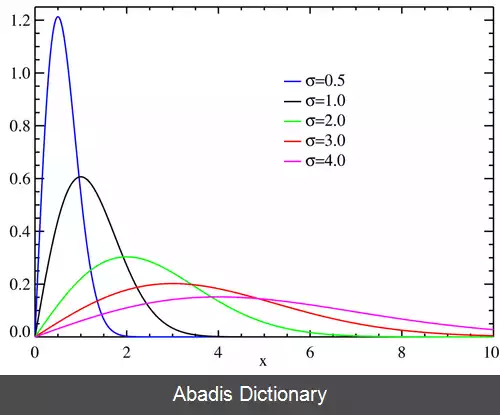
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتابع چگالی احتمال یک توزیع رایلی چنین است.
که در این رابطه σ پارامتر مقیاس توزیع نامیده می شود.
تابع توزیع تجمعی در توزیع رایلی برابر است با:
در حالی که . x ∈ [ 0 , ∞ )
میانه در توزیع رایلی برابر است با:
σ π 2
مد در توزیع رایلی برابر است با:
σ
میانگین یک توزیع رایلی برابر است با:
واریانس یک توزیع رایلی برابر است با:
4 − π 2 σ 2
توزیع رایلی معمولا برای مدل کردن ارتفاع موج ها در علوم اقیانوس شناسی استفاده می شود و همچنین برای بررسی بیشینه انرژی دریافتی از موج های رادیویی نیز استفاده می شود. در گذشته هم برای مدل سازی فرکانس سرعت باد در توربین های بادی در طول یک سال مورد استفاده واقع می شده است. [ ۱]
• R ∼ R a y l e i g h ( σ ) {\displaystyle R\sim \mathrm {Rayleigh} ( \sigma ) } اگر R = X 2 + Y 2 {\displaystyle R={\sqrt {X^{2}+Y^{2}}}} و X ∼ N ( 0 , σ 2 ) {\displaystyle X\sim N ( 0, \sigma ^{2} ) } و Y ∼ N ( 0 , σ 2 ) {\displaystyle Y\sim N ( 0, \sigma ^{2} ) } دو متغیر مستقل با توزیع نرمال باشند.


wiki: توزیع ریلی
