توزیع خی دو نامرکزی ( به انگلیسی: Noncentral chi - squared distribution ) تعمیمی از توزیع خی دو است؛ در حقیقت توزیع خی دو ( یا توزیع کی دو یا χ 2 ) حالت خاصی از توزیع خی دو نامرکزی است. [ ۱] درشاخهٔ آمار چندمتغیره و دیگر آمارها توزیع خی دو نامرکزی بسیار پرکاربرد است. این توزیع را معمولاً زمانی که فرض صفر در آزمون فرض آماری درست نباشد، می بینیم. [ ۲]
اگر ( X 1 , X 2 , . . . , X k ) k تا متغیر تصادفی مستقل باشند، به طوری که:
X i ∼ N ( μ i , σ i ) آنگاه متغیر تصادفی
∑ i = 1 k ( X i σ ) 2 از توزیع خی دو نامرکزی پیروی می کند:
∑ i = 1 k ( X i σ ) 2 ∼ χ 2 ( k , λ ) k درجه آزادی است که برابر تعداد X i هاست و λ مؤلفه میزان نامرکزی بودن ( به انگلیسی :Noncentrality paramete ) است که تعریفی به شکل زیر دارد:
λ = ∑ i = 1 k μ i 2 σ 2 با این تعریف وقتی λ = 0 باشد، توزیع همان توزیع خی دو خواهد بود. [ ۳]
برای تولید یک نمونه تصادفی از این توزیع می توانید فرایند شبه کد زیر را دنبال کنید:
برای k و λ مشخص ( k > = 1 ) :
قرار بده u = s q r t ( λ )
متغیر تصادفی z 1 ∼ N ( u , 1 ) را نمونه گیری کن
متغیر تصادفی y ∼ g a m m a ( ( k − 1 ) 2 , 2 ) را نمونه گیری کن
x = z 1 2 + y را برگردان
x یک متغیر تصادفی از توزیع χ 2 ( k , δ ) خواهد بود. [ ۴]
تابع چگالی احتمال توزیع خی دو نامرکزی با درجهٔ آزادی k و میزان نامرکزی بودن λ که با χ 2 ( k , λ ) آن را نشان می دهیم، به صورت زیر است:[ ۳]
f ( x ) = { e − 1 / 2 ( x + λ ) 2 k / 2 ∑ j = 0 ∞ x k / 2 + j − 1 λ j Γ ( k / 2 + j ) 2 2 j j ! 0 < x < ∞ 0 otherwise این تابع را به شکل های دیگر نیز می توان نوشت، همچون : f x ( k , λ ) = 1 / 2 e − ( x + k ) / 2 ( x λ ) k / 4 − 1 / 2 I k / 2 − 1 ( λ x ) که I v ( y ) در آن تابع بسل نوع اول است که برابر است با : I v ( y ) = ( y / 2 ) v ∑ j = 0 ∞ ( y 2 / 4 ) j j ! Γ ( v + j + 1 ) نمودار چگالی احتمال می توانید نمودار چگالی احتمال این توزیع را در شکل های زیر ببینید: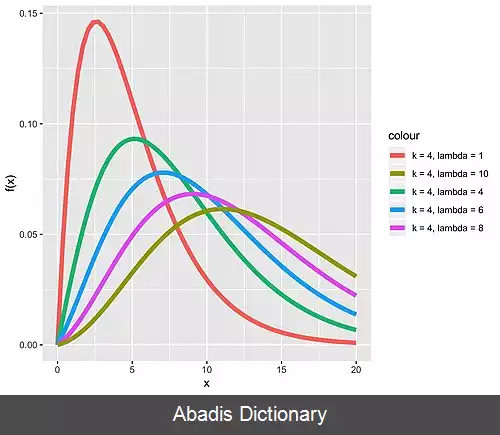
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر ( X 1 , X 2 , . . . , X k ) k تا متغیر تصادفی مستقل باشند، به طوری که:
X i ∼ N ( μ i , σ i ) آنگاه متغیر تصادفی
∑ i = 1 k ( X i σ ) 2 از توزیع خی دو نامرکزی پیروی می کند:
∑ i = 1 k ( X i σ ) 2 ∼ χ 2 ( k , λ ) k درجه آزادی است که برابر تعداد X i هاست و λ مؤلفه میزان نامرکزی بودن ( به انگلیسی :Noncentrality paramete ) است که تعریفی به شکل زیر دارد:
λ = ∑ i = 1 k μ i 2 σ 2 با این تعریف وقتی λ = 0 باشد، توزیع همان توزیع خی دو خواهد بود. [ ۳]
برای تولید یک نمونه تصادفی از این توزیع می توانید فرایند شبه کد زیر را دنبال کنید:
برای k و λ مشخص ( k > = 1 ) :
قرار بده u = s q r t ( λ )
متغیر تصادفی z 1 ∼ N ( u , 1 ) را نمونه گیری کن
متغیر تصادفی y ∼ g a m m a ( ( k − 1 ) 2 , 2 ) را نمونه گیری کن
x = z 1 2 + y را برگردان
x یک متغیر تصادفی از توزیع χ 2 ( k , δ ) خواهد بود. [ ۴]
تابع چگالی احتمال توزیع خی دو نامرکزی با درجهٔ آزادی k و میزان نامرکزی بودن λ که با χ 2 ( k , λ ) آن را نشان می دهیم، به صورت زیر است:[ ۳]
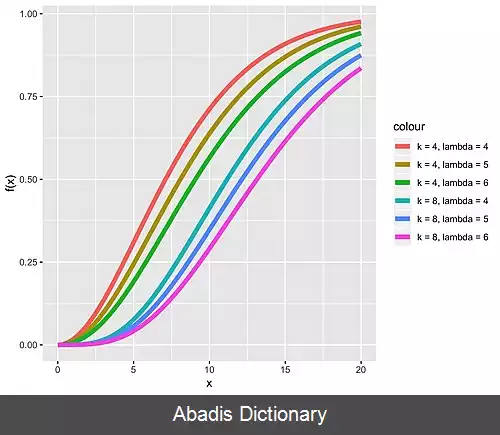
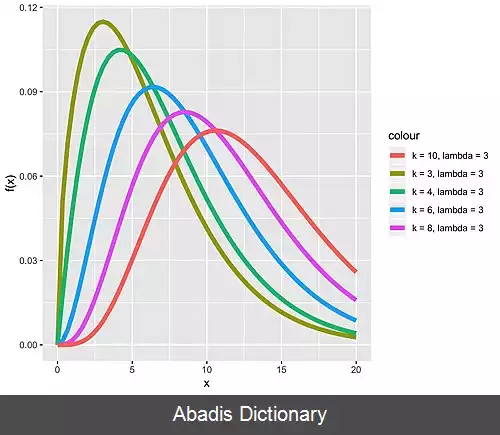
f ( x ) = { e − 1 / 2 ( x + λ ) 2 k / 2 ∑ j = 0 ∞ x k / 2 + j − 1 λ j Γ ( k / 2 + j ) 2 2 j j ! 0 < x < ∞ 0 otherwise این تابع را به شکل های دیگر نیز می توان نوشت، همچون : f x ( k , λ ) = 1 / 2 e − ( x + k ) / 2 ( x λ ) k / 4 − 1 / 2 I k / 2 − 1 ( λ x ) که I v ( y ) در آن تابع بسل نوع اول است که برابر است با : I v ( y ) = ( y / 2 ) v ∑ j = 0 ∞ ( y 2 / 4 ) j j ! Γ ( v + j + 1 ) نمودار چگالی احتمال می توانید نمودار چگالی احتمال این توزیع را در شکل های زیر ببینید:



wiki: توزیع خی دو نامرکزی
