توزیع خی دو
فرهنگستان زبان و ادب
دانشنامه عمومی
توزیع خی دو[ ۱] ( و یا کی دو یا χ 2 ) ( به انگلیسی: Chi - square distribution ) در نظریه احتمالات و آمار، دارای کاربرد وسیعی در آمار استنباطی است، به طور مثال در آزمون معناداری آماری. [ ۲] [ ۳] [ ۴]
γ ( a , x ) = ∫ 0 x t a − 1 e − t d t
درتئوری آمار و احتمال chi - square distribution با k درجه آزادی توزیعی است از یک سری مجموع مربعات متغیرهای تصادفی نرمال مستقل از هم ( یعنی شما یه توزیع نرمال داری ازش به طور تصادفی متغیرهایی رو برمی داری اینا رو به توان دو میرسونی و با هم جمع می کنی این میشه chi - square distribution )
chi - square distribution یک نمونه خاصی از توزیع گاماست؛ و در توزیع های احتمال در آمار استنباطی کاربرد زیادی دارد؛ به ویژه در hypothesis testing و ساختن نواحی اطمینان ( یک سیگما دو سیگما و… ) . این توزیع اغلب توزیع کای - اسکور مرکزی نامیده می شود؛ مورد خاصی از توزیع کای - اسکور عام غیر مرکزی است. chi - square distribution در تست های متداول فیتینگ از یک توزیع مشاهده شده با یک توزیع تیوریکال استفاده می شود.
مستقل از دو معیار: طبقه بندی کیفیت داده ها و برآورد فاصلهٔ اطمینان ( همون یک سیگما دو سیگما ) برای جمعیتی که انحراف استاندارش از یک توزیع نرمال برای یک نمونه انحراف استاندارد. بسیاری از آزمونهای آماری نیز از این توزیع استفاده می کنند مانند تحلیل فریدمان براساس رتبه ها.
رتبه بندی به کار می رود و نیز برای مقایسه میانگین رتبه بندی گروه های مختلف کاربرد دارد )
اگر Z1، … ، Zk متغیرهای تصادفی نرمال استاندارد و مستقل باشند، پس حاصل جمع مربعات آنها:
standard normal random variables
برطبق توزیع کای - اسکور با k درجه آزادی توزیع می شود. این معمولاً به صورت زیر نشان داده می شود:
توزیع کای - اسور دارای یک پارامتر است: یک عدد صحیح مثبت k که تعداد درجات آزادی ( تعداد Ziها ) را مشخص می کند.
توزیع کای - اسکور در درجه اول در hypothesis testing و به میزان کمتری برای فواصل اطمینان confidence intervals برای واریانس جمعیت هنگامی که توزیع نرمال هستند، استفاده می شود. برخلاف توزیع های مشهورتر مانند توزیع نرمال و توزیع نمایی، توزیع کای - اسکور به طور معمول در مدل سازی مستقیم پدیده های طبیعی اعمال نمی شود. این در آزمون فرضیه زیر وجود دارد: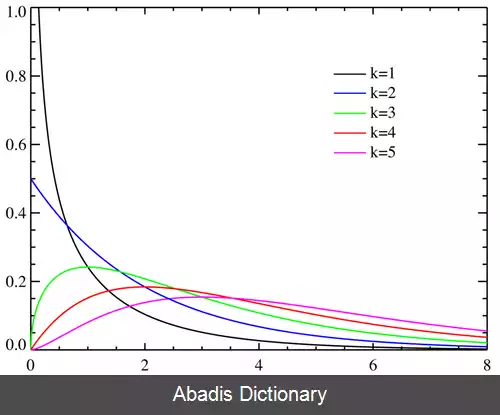
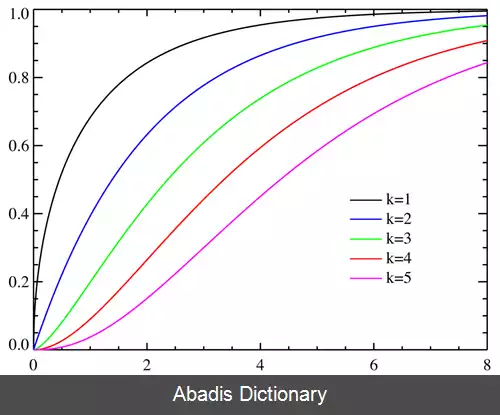
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفγ ( a , x ) = ∫ 0 x t a − 1 e − t d t
درتئوری آمار و احتمال chi - square distribution با k درجه آزادی توزیعی است از یک سری مجموع مربعات متغیرهای تصادفی نرمال مستقل از هم ( یعنی شما یه توزیع نرمال داری ازش به طور تصادفی متغیرهایی رو برمی داری اینا رو به توان دو میرسونی و با هم جمع می کنی این میشه chi - square distribution )
chi - square distribution یک نمونه خاصی از توزیع گاماست؛ و در توزیع های احتمال در آمار استنباطی کاربرد زیادی دارد؛ به ویژه در hypothesis testing و ساختن نواحی اطمینان ( یک سیگما دو سیگما و… ) . این توزیع اغلب توزیع کای - اسکور مرکزی نامیده می شود؛ مورد خاصی از توزیع کای - اسکور عام غیر مرکزی است. chi - square distribution در تست های متداول فیتینگ از یک توزیع مشاهده شده با یک توزیع تیوریکال استفاده می شود.
مستقل از دو معیار: طبقه بندی کیفیت داده ها و برآورد فاصلهٔ اطمینان ( همون یک سیگما دو سیگما ) برای جمعیتی که انحراف استاندارش از یک توزیع نرمال برای یک نمونه انحراف استاندارد. بسیاری از آزمونهای آماری نیز از این توزیع استفاده می کنند مانند تحلیل فریدمان براساس رتبه ها.
رتبه بندی به کار می رود و نیز برای مقایسه میانگین رتبه بندی گروه های مختلف کاربرد دارد )
اگر Z1، … ، Zk متغیرهای تصادفی نرمال استاندارد و مستقل باشند، پس حاصل جمع مربعات آنها:
standard normal random variables
برطبق توزیع کای - اسکور با k درجه آزادی توزیع می شود. این معمولاً به صورت زیر نشان داده می شود:
توزیع کای - اسور دارای یک پارامتر است: یک عدد صحیح مثبت k که تعداد درجات آزادی ( تعداد Ziها ) را مشخص می کند.
توزیع کای - اسکور در درجه اول در hypothesis testing و به میزان کمتری برای فواصل اطمینان confidence intervals برای واریانس جمعیت هنگامی که توزیع نرمال هستند، استفاده می شود. برخلاف توزیع های مشهورتر مانند توزیع نرمال و توزیع نمایی، توزیع کای - اسکور به طور معمول در مدل سازی مستقیم پدیده های طبیعی اعمال نمی شود. این در آزمون فرضیه زیر وجود دارد:


wiki: توزیع خی دو
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
