توزیع حاشیه ای
فرهنگستان زبان و ادب
دانشنامه عمومی
در نظریه آمار و احتمال، توزیع حاشیه ای از یک زیرمجموعه از یک مجموعه ای از متغیرهای تصادفی، توزیع احتمال از متغیرهای موجود در زیر مجموعه هست. احتمال مقادیر مختلف متغیرها را در زیرمجموعه بدون مراجعه به مقادیر سایر متغیرها ارائه می دهد. در حالی که توزیع شرطی، احتمالات را مشروط به مقادیر متغیرهای دیگر می کند.
متغیرهای حاشیه ای آن متغیرها در زیرمجموعه متغیرهایی هستند که حفظ می شوند. این مفاهیم «حاشیه ای» هستند زیرا با جمع کردن مقادیر در جدول در امتداد سطرها یا ستون ها و نوشتن حاصل جمع در حاشیه جدول، می توان آنها را یافت. [ ۱] توزیع متغیرهای حاشیه ای ( توزیع حاشیه ای ) توسط حاشیه سازی حاصل می شود، یعنی تمرکز روی مبالغ موجود در حاشیه بیش از توزیع متغیرهای کنار گذاشته شده است، و گفته می شود که متغیرهای دور انداخته شده، به حاشیه رانده شده اند.
به طور ساده تر گاهی نیاز داریم توزیع مستقل دو متغیر تصادفی را هم از توزیع توأم به دست آوریم. جواب این سؤال ما در توزیع حاشیه ای نهفته است.
برای حساب کردن توزیع حاشیه ای یکی از این متغیرها کافی است به نوعی تأثیر آنرا بر روی تابع توزیع توأم حذف کنیم.
فرض کنید توزیع توأم[ ۲] دو متغیر تصادفی گسسته X و Y به ما داده شده است. توزیع حاشیه ای هر یک از این متغیرها - به عنوان مثال X - برابر است با توزیع احتمال X هنگامی که مقادیر Y در نظر گرفته نمی شوند. این را می توان با جمع کردن احتمال توزیع توأم روی تمام حالات Y محاسبه کرد. به طور مشابه، برای عکس آن نیز درست است؛ یعنی توزیع حاشیه ای Y را نیز می توان با جمع کردن احتمال توزیع توأم روی حالات X محاسبه کرد.
p X ( x i ) = ∑ j p ( x i , y j )
p Y ( y j ) = ∑ i p ( x i , y j )
احتمال حاشیه ای می تواند به صورت امید ریاضی نیز نوشته شود.
p X ( x ) = ∫ y p X ∣ Y ( x ∣ y ) p Y ( y ) d y = E Y به طور شهودی احتمال حاشیه ای X با بررسی احتمال شرطی X به شرط مقدار خاصی از Y، و سپس میانگین این احتمال شرطی بر روی توزیع همه مقادیر Y محاسبه می شود.
این از تعریف امید ریاضی ( بعد از انجام قانون LOTUS ) می آید.
E Y = ∫ y f ( y ) p Y ( y ) d y تابع چگالی احتمال حاشیه ای فرض کنید توزیع توأم دو متغیر تصادفی پیوسته X و Y به ما داده شده است. تابع چگالی احتمال حاشیه ای X را می توان از انتگرال احتمال توزیع توأم روی تمام حالات Y محاسبه کرد.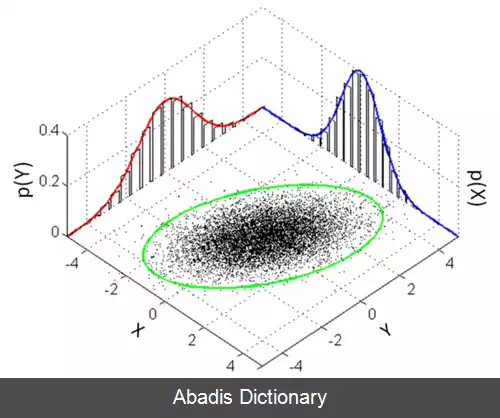
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمتغیرهای حاشیه ای آن متغیرها در زیرمجموعه متغیرهایی هستند که حفظ می شوند. این مفاهیم «حاشیه ای» هستند زیرا با جمع کردن مقادیر در جدول در امتداد سطرها یا ستون ها و نوشتن حاصل جمع در حاشیه جدول، می توان آنها را یافت. [ ۱] توزیع متغیرهای حاشیه ای ( توزیع حاشیه ای ) توسط حاشیه سازی حاصل می شود، یعنی تمرکز روی مبالغ موجود در حاشیه بیش از توزیع متغیرهای کنار گذاشته شده است، و گفته می شود که متغیرهای دور انداخته شده، به حاشیه رانده شده اند.
به طور ساده تر گاهی نیاز داریم توزیع مستقل دو متغیر تصادفی را هم از توزیع توأم به دست آوریم. جواب این سؤال ما در توزیع حاشیه ای نهفته است.
برای حساب کردن توزیع حاشیه ای یکی از این متغیرها کافی است به نوعی تأثیر آنرا بر روی تابع توزیع توأم حذف کنیم.
فرض کنید توزیع توأم[ ۲] دو متغیر تصادفی گسسته X و Y به ما داده شده است. توزیع حاشیه ای هر یک از این متغیرها - به عنوان مثال X - برابر است با توزیع احتمال X هنگامی که مقادیر Y در نظر گرفته نمی شوند. این را می توان با جمع کردن احتمال توزیع توأم روی تمام حالات Y محاسبه کرد. به طور مشابه، برای عکس آن نیز درست است؛ یعنی توزیع حاشیه ای Y را نیز می توان با جمع کردن احتمال توزیع توأم روی حالات X محاسبه کرد.
p X ( x i ) = ∑ j p ( x i , y j )
p Y ( y j ) = ∑ i p ( x i , y j )
احتمال حاشیه ای می تواند به صورت امید ریاضی نیز نوشته شود.
p X ( x ) = ∫ y p X ∣ Y ( x ∣ y ) p Y ( y ) d y = E Y به طور شهودی احتمال حاشیه ای X با بررسی احتمال شرطی X به شرط مقدار خاصی از Y، و سپس میانگین این احتمال شرطی بر روی توزیع همه مقادیر Y محاسبه می شود.
این از تعریف امید ریاضی ( بعد از انجام قانون LOTUS ) می آید.
E Y = ∫ y f ( y ) p Y ( y ) d y تابع چگالی احتمال حاشیه ای فرض کنید توزیع توأم دو متغیر تصادفی پیوسته X و Y به ما داده شده است. تابع چگالی احتمال حاشیه ای X را می توان از انتگرال احتمال توزیع توأم روی تمام حالات Y محاسبه کرد.

wiki: توزیع حاشیه ای
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
