در ریاضیات، توابع زوج و توابع فرد، توابعی هستند که در مورد بعضی روابط قرینگی، در رابطه با وارون های افزایشی به بحث می پردازد. این توابع در بسیاری از زمینه های آنالیز ریاضی کاربرد دارند، خصوصاً در مورد تئوری سری های توانی و دستورالعمل سری فوریه. این توابع به دلیل مشابهت توان های توابع توانی که هر دو شرایط را به خدمت می گیرند نام گذاری شده اند: تابع xn تابعی زوج است اگر n یک عدد صحیح زوج باشد و در صورتی که n عدد صحیح فردی باشد، تابعی فرد است.
فرض می کنیم f ( x ) تابعی حقیقی باشد. آن گاه f، زوج است اگر رابطهٔ زیر برای تمام xهای در دامنهٔ f برقرار باشد:
: f ( x ) = f ( − x ) .
به طور هندسی، یک تابع زوج، نسبت به محور yها قرینه است، که معنی آن این است که با بازتاباندن هر قسمتی از تابع نسبت به محور yها، تابع بدون تغییر بماند.
مثال هایی از توابع زوج، تابع ثابت f ( x ) = c ، x2 ، x4 ، cos ( x ) ، و cosh ( x ) می باشند.
فرض می کنیم f ( x ) تابعی حقیقی باشد. آن گاه f، فرد است اگر رابطهٔ زیر برای تمام xهای در دامنهٔ f برقرار باشد:
: − f ( x ) = f ( − x ) .
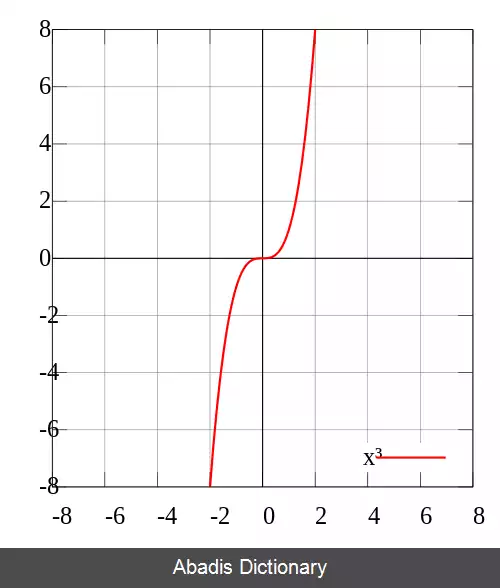
به طور هندسی، یک تابع فرد، نسبت به مبدأ مختصات تقارن دارد، که معنی آن این است که تابع بعد از چرخشی ۱۸۰ درجه ای، بدون تغییر می ماند. در واقع مبدا مختصات نقطه عطف این نوع تابع ها می باشد.
مثال هایی از تابع فرد، تابع همانی f ( x ) = x ، x3 ، sin ( x ) و sinh ( x ) می باشند.
• تنها تابعی که هم زوج و هم فرد است، تابع ثابت صفر است. ( برای مثال برای هر x داریم: f ( x ) = ۰ )
• مجموع یک تابع زوج و یک تابع فرد، نه زوج است نه فرد، مگر یکی از آن ها عیناً صفر باشد.
• مجموع دو تابع زوج، تابعی زوج است، و حاصلضرب هر عدد ثابت در یک تابع زوج هر عدد قابل ضرب
• حاصل ضرب یک تابع زوج و یک تابع فرد، تابعی فرد است.
• حاصل تقسیم دو تابع زوج، تابعی زوج است.
• حاصل تقسیم دو تابع فرد، تابعی زوج است.
• حاصل تقسیم یک تابع زوج و یک تابع فرد، تابعی فرد است.
• مشتق یک تابع زوج، تابعی فرد است.
• مشتق یک تابع فرد، تابعی زوج است.
• ترکیب دو تابع زوج، تابعی زوج است، و ترکیب دو تابع فرد، تابعی فرد است.
• ترکیب یک تابع زوج و یک تابع فرد، تابعی زوج است.
• ترکیب هر تعداد تابعی که در میان آن ها حداقل یک تابع زوج وجود داشته باشد، تابعی زوج است ( اما نه به عکس ) .
• انتگرال یک تابع فرد از A - تا A+، صفر است ( در صورتی که A کران دار باشد، و تابع در فاصلهٔ A - تا A+، هیچ مجانب قائمی نداشته باشد ) .
• انتگرال یک تابع زوج از A - تا A+، دوبرابر انتگرال از ۰ تا A+ است ( در صورتی که A کران دار باشد، و تابع در فاصلهٔ A - تا A+، هیچ مجانب قائمی نداشته باشد ) .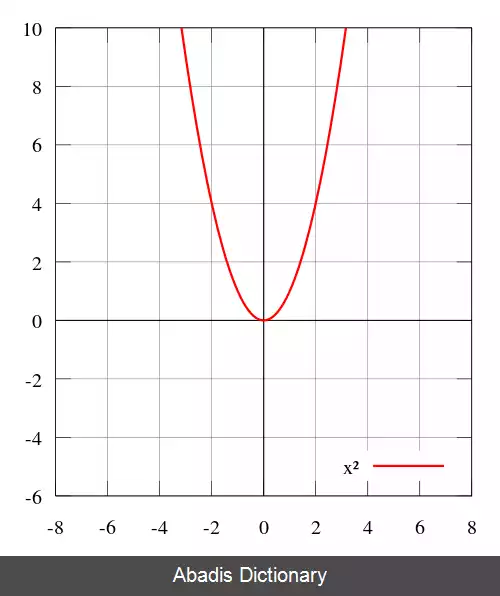
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض می کنیم f ( x ) تابعی حقیقی باشد. آن گاه f، زوج است اگر رابطهٔ زیر برای تمام xهای در دامنهٔ f برقرار باشد:
: f ( x ) = f ( − x ) .
به طور هندسی، یک تابع زوج، نسبت به محور yها قرینه است، که معنی آن این است که با بازتاباندن هر قسمتی از تابع نسبت به محور yها، تابع بدون تغییر بماند.
مثال هایی از توابع زوج، تابع ثابت f ( x ) = c ، x2 ، x4 ، cos ( x ) ، و cosh ( x ) می باشند.
فرض می کنیم f ( x ) تابعی حقیقی باشد. آن گاه f، فرد است اگر رابطهٔ زیر برای تمام xهای در دامنهٔ f برقرار باشد:
: − f ( x ) = f ( − x ) .
به طور هندسی، یک تابع فرد، نسبت به مبدأ مختصات تقارن دارد، که معنی آن این است که تابع بعد از چرخشی ۱۸۰ درجه ای، بدون تغییر می ماند. در واقع مبدا مختصات نقطه عطف این نوع تابع ها می باشد.
مثال هایی از تابع فرد، تابع همانی f ( x ) = x ، x3 ، sin ( x ) و sinh ( x ) می باشند.
• تنها تابعی که هم زوج و هم فرد است، تابع ثابت صفر است. ( برای مثال برای هر x داریم: f ( x ) = ۰ )
• مجموع یک تابع زوج و یک تابع فرد، نه زوج است نه فرد، مگر یکی از آن ها عیناً صفر باشد.
• مجموع دو تابع زوج، تابعی زوج است، و حاصلضرب هر عدد ثابت در یک تابع زوج هر عدد قابل ضرب
• حاصل ضرب یک تابع زوج و یک تابع فرد، تابعی فرد است.
• حاصل تقسیم دو تابع زوج، تابعی زوج است.
• حاصل تقسیم دو تابع فرد، تابعی زوج است.
• حاصل تقسیم یک تابع زوج و یک تابع فرد، تابعی فرد است.
• مشتق یک تابع زوج، تابعی فرد است.
• مشتق یک تابع فرد، تابعی زوج است.
• ترکیب دو تابع زوج، تابعی زوج است، و ترکیب دو تابع فرد، تابعی فرد است.
• ترکیب یک تابع زوج و یک تابع فرد، تابعی زوج است.
• ترکیب هر تعداد تابعی که در میان آن ها حداقل یک تابع زوج وجود داشته باشد، تابعی زوج است ( اما نه به عکس ) .
• انتگرال یک تابع فرد از A - تا A+، صفر است ( در صورتی که A کران دار باشد، و تابع در فاصلهٔ A - تا A+، هیچ مجانب قائمی نداشته باشد ) .
• انتگرال یک تابع زوج از A - تا A+، دوبرابر انتگرال از ۰ تا A+ است ( در صورتی که A کران دار باشد، و تابع در فاصلهٔ A - تا A+، هیچ مجانب قائمی نداشته باشد ) .


wiki: توابع زوج و فرد
