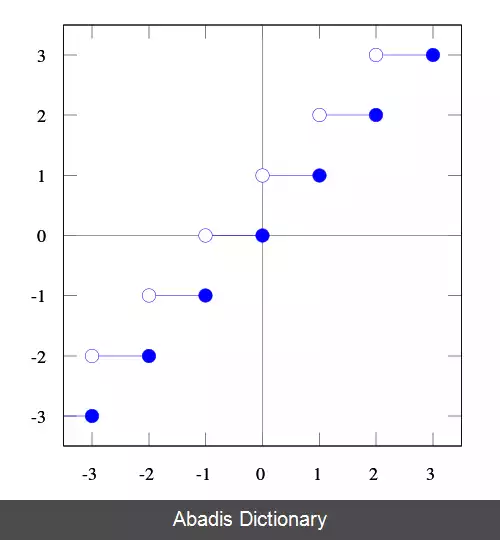
در ریاضیات و علوم کامپیوتر دو تابع «جزء صحیح یا کف ( یا براکت ) » و «سقف» توابعی هستند که به ترتیب هر مقدار حقیقی که به آن ها داده شود را به بزرگترین عدد صحیح کوچکتر ( یا مساوی ) و کوچکترین عدد صحیح بزرگتر ( یا مساوی ) گرد می کنند. به عبارت دیگر تابع جزء صحیح که به صورت ⌊ x ⌋ نمایش داده می شود به بزرگترین عدد صحیح قبل از آن گرد می کند یعنی به طور مثال ۲٫۶ را به ۲ و ۳٫۴ - را به ۴ - گرد می کند اما تابع سقف که به صورت ⌈ x ⌉ نمایش داده می شود به کوچکترین عدد صحیح بعد از آن گرد می کند یعنی ۲٫۶ را به ۳ و ۳٫۴ - را به ۳ - گرد می کند. [ ۱]
گاوس ریاضی دان آلمانی، نماد براکت گوشه دار را در اثبات قانون تقابل درجه دوم برای نمایش «تابع جزءِ صحیح» معرفی نمود ( سال ۱۸۰۸ میلادی ) که تا ارائهٔ نماد جدید کنت ای آیورسن به صورت استاندارد استفاده می شد. کنت ای آیورسن اصطلاحات «کف» و «سقف» را با نمادگذاری به صورت ⌊ x ⌋ و ⌈ x ⌉ در کتاب زبان برنامه نویسی اش ارائه نمود ( سال ۱۹۹۶ ) . گرچه استاندارد نمادگذاری مطابق با نمادگذاری «آیورسن» است اما در ریاضیات امروزی از هر دو نمادگذاری استفاده می گردد. [ ۲]
تعریف ریاضیاتی جزء صحیح به شرح زیر است:
⌊ x ⌋ = m a x { n ∈ Z ′ | n ≤ x }
معنی آن به زبان عامیانه این است: جزء صحیح X بیشترین عدد صحیحی است که کمتر یا مساوی X است.
بعضی مواقع جزء صحیح یک عدد را به صورت هم نشان می دهند.
آنگاه
If:z< x< y➡=z
یعنی هرگاه xبین z و y باشد جزء صحیح آن برابر مقدار کوچک تر ( z ) است
مثال:
x=1. 9999➡=1
x=1. 00001 ➡=1
x= - 1. 01➡ = - 2
x= - 1. 99➡ = - 2
برخی از اتحادهای معروف:
A ) ⌊ x ⌋ ≤ x < ⌊ x ⌋ + 1
.
B ) { x = ⌊ x ⌋ + { x } ⌊ x ⌋ ∈ Z ′ 0 ≤ { x } < 1 ===== ==> هر عددی از یک جزء صحیح و یک جزء کسری تشکیل شده است.
C ) { ⌊ x + K ⌋ = ⌊ x ⌋ + K K ∈ Z ′ , x ∈ R ′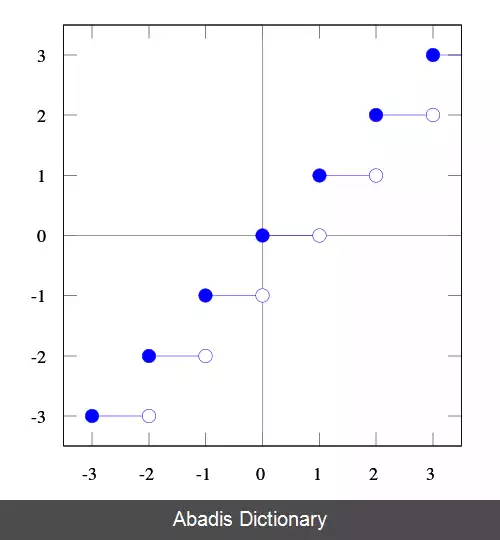
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگاوس ریاضی دان آلمانی، نماد براکت گوشه دار را در اثبات قانون تقابل درجه دوم برای نمایش «تابع جزءِ صحیح» معرفی نمود ( سال ۱۸۰۸ میلادی ) که تا ارائهٔ نماد جدید کنت ای آیورسن به صورت استاندارد استفاده می شد. کنت ای آیورسن اصطلاحات «کف» و «سقف» را با نمادگذاری به صورت ⌊ x ⌋ و ⌈ x ⌉ در کتاب زبان برنامه نویسی اش ارائه نمود ( سال ۱۹۹۶ ) . گرچه استاندارد نمادگذاری مطابق با نمادگذاری «آیورسن» است اما در ریاضیات امروزی از هر دو نمادگذاری استفاده می گردد. [ ۲]
تعریف ریاضیاتی جزء صحیح به شرح زیر است:
⌊ x ⌋ = m a x { n ∈ Z ′ | n ≤ x }
معنی آن به زبان عامیانه این است: جزء صحیح X بیشترین عدد صحیحی است که کمتر یا مساوی X است.
بعضی مواقع جزء صحیح یک عدد را به صورت هم نشان می دهند.
آنگاه
If:z< x< y➡=z
یعنی هرگاه xبین z و y باشد جزء صحیح آن برابر مقدار کوچک تر ( z ) است
مثال:
x=1. 9999➡=1
x=1. 00001 ➡=1
x= - 1. 01➡ = - 2
x= - 1. 99➡ = - 2
برخی از اتحادهای معروف:
A ) ⌊ x ⌋ ≤ x < ⌊ x ⌋ + 1
.
B ) { x = ⌊ x ⌋ + { x } ⌊ x ⌋ ∈ Z ′ 0 ≤ { x } < 1 ===== ==> هر عددی از یک جزء صحیح و یک جزء کسری تشکیل شده است.
C ) { ⌊ x + K ⌋ = ⌊ x ⌋ + K K ∈ Z ′ , x ∈ R ′


wiki: توابع جزء صحیح و سقف
