یک تعریف بازگشتی ( یا تعریف استقرایی ) در منطق ریاضی و علوم کامپیوتر برای تعریف اعضای یک مجموعه به طور وابسته به دیگر اعضا استفاده می شود. یک رابطه بازگشتی فرمولی است که جملهٔ n ام را به k جملهٔ پیشین مرتبط می سازد.
تعریف بازگشتی یک تابع مقادیر تابع را برای برخی از ورودی ها با در نظر گرفتن اعضای دیگری از همین تابع بیان می کند. برای مثال تابع فاکتوریل ( n ! ) با دستور زیر تعریف می شود:
0 ! = 1
( n + 1 ) ! = ( n ! ) ( n + 1 ) این تعریف برای هر n برقرار است. زیرا با بازگشتن پیاپی از حالت نهایی به سمت عقب، نهایتاً به جملهٔ اولیهٔ صفر می رسیم. به عبارتی، این تعریف یک روند برای ساخت تابع n ! بیان می کند که با شروع از n = 0 و ادامه دادن با n = 1 و n = 2 و … به جملهٔ مورد نظر از این دنباله می رسیم.
همان طور که گفته شد، تعریف استقرایی یک مجموعه هر عضو مجموعه را بر اساس دیگر اعضای موجود در مجموعه توصیف می کند. برای مثال یک تعریف از مجموعهٔ اعداد طبیعی ( N ) در اینجا ارائه شده است:
• عدد 1 {\displaystyle 1} عضوی از N {\displaystyle \mathbb {N} } است.
• اگر یک عنصر n {\displaystyle n} عضو N {\displaystyle \mathbb {N} } باشد، n + 1 {\displaystyle n+1} نیز عضوی از N {\displaystyle \mathbb {N} } است.
• N {\displaystyle \mathbb {N} } اشتراک تمام مجموعه هایی ست که در شروط بالا صدق کند.
مجموعه های بسیاری در شروط ۱ و ۲ صدق می کنند. مثلاً مجموعهٔ زیر را در نظر بگیرید: { 1 , 1. 649 , 2 , 2. 649 , 3 , 3. 649 , . . . } این مجموعه در شروط یک و دو ی بالا صدق می کند. اما شرط سه مجموعهٔ اعداد طبیعی را با حذف اعضای فرعی به وجود می آورد.
ویژگی های توابع و مجموعه های تعریف شده به صورت بازگشتی را اغلب می توان با استقرای ریاضی ثابت کرد. برای مثال تعریف اعداد طبیعی ارائه شده در اینجا به طور مستقیم به اصل استقرای ریاضی برای اعداد طبیعی دلالت می کند: اگر یک ویژگی برای عدد ۰ برقرار باشد و از برقراری آن ویژگی برای n بتوان درستی آن را برای n + 1 نیز نشان داد، آن ویژگی برای تمام اعداد طبیعی برقرار خواهد بود.
اکثر تعاریف بازگشتی بر دو اساس استوارند: یک یا چند جملهٔ پایه و یک شرط استقرایی.
تفاوت بین تعریف دایره ای و تعریف بازگشتی این است که یک تعریف بازگشتی باید همیشه حالت پایه داشته باشد. در مقابل یک تعریف دایره ای هیچ پایه ای ندارد و مقدار یک تابع را با توجه به خود آن تعریف می کند. این باعث می شود که تا بی نهایت مجبور به بازگشت باشیم.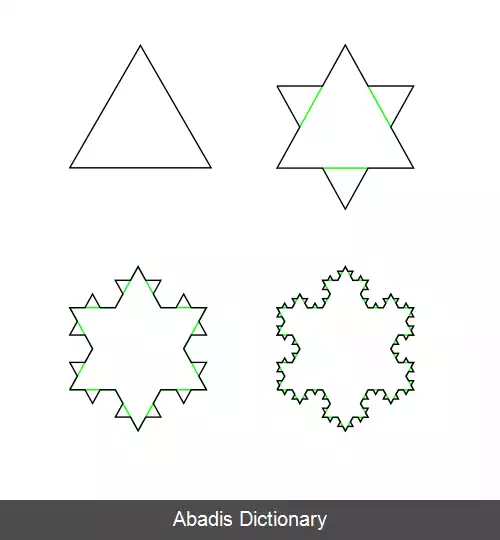
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتعریف بازگشتی یک تابع مقادیر تابع را برای برخی از ورودی ها با در نظر گرفتن اعضای دیگری از همین تابع بیان می کند. برای مثال تابع فاکتوریل ( n ! ) با دستور زیر تعریف می شود:
0 ! = 1
( n + 1 ) ! = ( n ! ) ( n + 1 ) این تعریف برای هر n برقرار است. زیرا با بازگشتن پیاپی از حالت نهایی به سمت عقب، نهایتاً به جملهٔ اولیهٔ صفر می رسیم. به عبارتی، این تعریف یک روند برای ساخت تابع n ! بیان می کند که با شروع از n = 0 و ادامه دادن با n = 1 و n = 2 و … به جملهٔ مورد نظر از این دنباله می رسیم.
همان طور که گفته شد، تعریف استقرایی یک مجموعه هر عضو مجموعه را بر اساس دیگر اعضای موجود در مجموعه توصیف می کند. برای مثال یک تعریف از مجموعهٔ اعداد طبیعی ( N ) در اینجا ارائه شده است:
• عدد 1 {\displaystyle 1} عضوی از N {\displaystyle \mathbb {N} } است.
• اگر یک عنصر n {\displaystyle n} عضو N {\displaystyle \mathbb {N} } باشد، n + 1 {\displaystyle n+1} نیز عضوی از N {\displaystyle \mathbb {N} } است.
• N {\displaystyle \mathbb {N} } اشتراک تمام مجموعه هایی ست که در شروط بالا صدق کند.
مجموعه های بسیاری در شروط ۱ و ۲ صدق می کنند. مثلاً مجموعهٔ زیر را در نظر بگیرید: { 1 , 1. 649 , 2 , 2. 649 , 3 , 3. 649 , . . . } این مجموعه در شروط یک و دو ی بالا صدق می کند. اما شرط سه مجموعهٔ اعداد طبیعی را با حذف اعضای فرعی به وجود می آورد.
ویژگی های توابع و مجموعه های تعریف شده به صورت بازگشتی را اغلب می توان با استقرای ریاضی ثابت کرد. برای مثال تعریف اعداد طبیعی ارائه شده در اینجا به طور مستقیم به اصل استقرای ریاضی برای اعداد طبیعی دلالت می کند: اگر یک ویژگی برای عدد ۰ برقرار باشد و از برقراری آن ویژگی برای n بتوان درستی آن را برای n + 1 نیز نشان داد، آن ویژگی برای تمام اعداد طبیعی برقرار خواهد بود.
اکثر تعاریف بازگشتی بر دو اساس استوارند: یک یا چند جملهٔ پایه و یک شرط استقرایی.
تفاوت بین تعریف دایره ای و تعریف بازگشتی این است که یک تعریف بازگشتی باید همیشه حالت پایه داشته باشد. در مقابل یک تعریف دایره ای هیچ پایه ای ندارد و مقدار یک تابع را با توجه به خود آن تعریف می کند. این باعث می شود که تا بی نهایت مجبور به بازگشت باشیم.

wiki: تعریف بازگشتی
